题目内容
对于一切x∈[-2,
],不等式ax3-x2+x+1≥0恒成立,求实数a的取值范围.
| 1 |
| 2 |
考点:函数恒成立问题
专题:导数的综合应用
分析:分x=0,x>0,x<0三种情况讨论,分离参数a后利用导数求函数的最值,从而求得实数a的取值范围.
解答:
解:当x=0时,对于任意实数a不等式ax3-x2+x+1≥0恒成立;
当0<x≤
时,不等式ax3-x2+x+1≥0等价于a≥-
-
+
.
设t=
(t≥2),则f(t)=-t3-t2+t,f′(t)=-3t2-2t+1=-(t+1)(3t-1),
当t≥2时,f′(t)<0,∴f(t)=-t3-t2+t为减函数,∴f(t)max=f(2)=-10,
∴a≥-10;
当-2≤x<0时,不等式ax3-x2+x+1≥0等价于a≤-
-
+
.
设t=
(t≤-
),则f(t)=-t3-t2+t,f′(t)=-3t2-2t+1=-(t+1)(3t-1),
当t∈(-∞,-1)时,f′(t)<0,f(t)为减函数,当t∈(-1,-
)时,f′(t)>0,f(t)为增函数,
∴f(t)min=f(-1)=-1.
∴a≤-1.
综上,对于一切x∈[-2,
],使不等式ax3-x2+x+1≥0恒成立的实数a的取值范围是[-10,-1].
当0<x≤
| 1 |
| 2 |
| 1 |
| x3 |
| 1 |
| x2 |
| 1 |
| x |
设t=
| 1 |
| x |
当t≥2时,f′(t)<0,∴f(t)=-t3-t2+t为减函数,∴f(t)max=f(2)=-10,
∴a≥-10;
当-2≤x<0时,不等式ax3-x2+x+1≥0等价于a≤-
| 1 |
| x3 |
| 1 |
| x2 |
| 1 |
| x |
设t=
| 1 |
| x |
| 1 |
| 2 |
当t∈(-∞,-1)时,f′(t)<0,f(t)为减函数,当t∈(-1,-
| 1 |
| 2 |
∴f(t)min=f(-1)=-1.
∴a≤-1.
综上,对于一切x∈[-2,
| 1 |
| 2 |
点评:本题考查恒成立问题,考查分类讨论的数学思想方法和数学转化思想方法,训练了利用导数求函数的最值,属中高档题.

练习册系列答案
相关题目
二项式(
-
)n的展开式中第4项为常数项,则常数项为( )
| x |
| 1 | |||
|
| A、10 | B、-10 |
| C、20 | D、-20 |

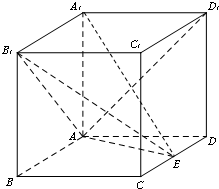 在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为线段CD中点.
在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为线段CD中点.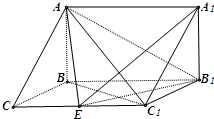 如图,在三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,∠BCC1=90°,AB⊥侧面BB1C1C.
如图,在三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,∠BCC1=90°,AB⊥侧面BB1C1C. 根据如图所示的三视图画出对应的几何体.
根据如图所示的三视图画出对应的几何体. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.