题目内容

18．已知集合U={1，2，3，4，5，6}，集合A={2，3}，集合B={1，2，4}，则（∁UB）∩A=（　　）
A．{2}B．{3}C．{5，6}D．{3，5，6}

分析 先求出CUB={3，5，6}，由此能求出（∁UB）∩A．

解答 解：∵集合U={1，2，3，4，5，6}，
集合A={2，3}，集合B={1，2，4}，
∴CUB={3，5，6}，
（∁UB）∩A={3}．
故选：B．

点评 本题考查补集、交集的求法，是基础题，解题时要认真审题，注意交集、并集、补集性质的合理运用．

练习册系列答案
相关题目
8．命题“?x∈[-2，+∞），x+3≥1”的否定为（　　）
A．?x0∈[-2，+∞），x0+3＜1B．?x0∈[-2，+∞），x0+3≥1
C．?0∈[-2，+∞），x0+3＜1D．?x0∈（-∞，-2），x0+3≥1
9．已知函数f（x）=|x-2|-4，g（x）=|x+1|-3．
（Ⅰ）若f（x）≤1，求实数x的取值范围；
（Ⅱ）若不等式f（x）-g（x）≥m-1有解，求实数m的取值范围．
6．已知双曲线经过点$（{1，2\sqrt{2}}）$，其一条渐近线方程为y=2x，则该双曲线的标准方程为$\frac{{y}^{2}}{4}$-x2=1．
13．已知向量$\overrightarrow m=（\sqrt{3}sin\frac{x}{4}，1），\overrightarrow n=（cos\frac{x}{4}，cos_{\;}^2\frac{x}{4}）．记f（x）=\overrightarrow m•\overrightarrow n$．
（1）若f（α）=$\frac{3}{2}，求cos（\frac{2π}{3}-α）$的值；
（2）在△ABC中，角A、B、C的对边分别是a、b、c，且满足（2a-c）cos B=bcos C，若f（A）=$\frac{{1+\sqrt{3}}}{2}$，试判断△ABC的形状．
3．已知函数f（x）（x∈R，且x≠1）的图象关于点（1，0）对称，当x＞1时f（x）=loga（x-1），且f（3）=-1，则不等式f（x）＞1的解集是（　　）
A．$（-3，\frac{3}{2}）$B．$（-∞，-3）∪（\frac{3}{2}，+∞）$C．$（-∞，-1）∪（\frac{3}{2}，+∞）$D．$（-∞，-1）∪（1，\frac{3}{2}）$
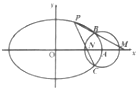10．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的长轴长为4，焦距为$2\sqrt{3}$，以A为圆心的圆（x-2）2+y2=r2（r＞0）与椭圆相交于B、C两点．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）求$\overrightarrow{AB}•\overrightarrow{AC}$的取值范围；
（Ⅲ）设P是椭圆C长异于B、C的任一点，直线PB、PC与x轴分别交于M、N，
求S△POM•S△PON的最大值．
7．求下列各式的值．
（Ⅰ）9${\;}^{\frac{1}{2}}$+（$\frac{1}{2}$）-1-lg100；
（Ⅱ）（2a${\;}^{\frac{2}{3}}$b${\;}^{\frac{1}{2}}$）（-6a${\;}^{\frac{1}{2}}$b${\;}^{\frac{1}{3}}$）÷（-3a${\;}^{\frac{1}{6}}$b${\;}^{\frac{5}{6}}$）．
8．已知函数f（x）=ax3+（3-a）x在[-1，1]上的最大值为3，则实数a的取值范围是（　　）
A．[-$\frac{3}{2}$，3]B．[-$\frac{3}{2}$，12]C．[-3，3]D．[-3，12]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网