题目内容
8.命题“?x∈[-2,+∞),x+3≥1”的否定为( )| A. | ?x0∈[-2,+∞),x0+3<1 | B. | ?x0∈[-2,+∞),x0+3≥1 | ||
| C. | ?0∈[-2,+∞),x0+3<1 | D. | ?x0∈(-∞,-2),x0+3≥1 |
分析 全称命题的否定是特称命题,直接写出结果即可.
解答 解:∵全称命题的否定是特称命题,
∴命题“?x∈[-2,+∞),x+3≥1”的否定是?x0∈[-2,+∞),x0+3<1,
故选:A.
点评 本题考查命题的否定,全称命题与特称命题的关系,基本知识的考查,注意命题的否定与否命题的区别.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
4.已知函数f(x)=$\frac{sinx}{2+cosx}$,如果当x>0时,若函数f(x)的图象恒在直线y=kx的下方,则k的取值范围是( )
| A. | [$\frac{1}{3}$,$\frac{\sqrt{3}}{3}$] | B. | [$\frac{1}{3}$,+∞) | C. | [$\frac{\sqrt{3}}{3}$,+∞) | D. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] |
5.已知命题p:△ABC中,若A>B,则cosA>cosB,则下列命题为真命题的是( )
| A. | p的逆命题 | B. | p的否命题 | C. | p的逆否命题 | D. | p的否定 |
3.已知圆C:x2+y2-4x+m=0与圆${({x-3})^2}+{({y+2\sqrt{2}})^2}=4$外切,点P是圆C一动点,则点P到直线3x-4y+4=0的距离的最大值为( )
| A. | $2\sqrt{2}$ | B. | 3 | C. | 4 | D. | $3\sqrt{2}$ |
20.若存在正实数m,使得关于x的方程x+a(2x+2m-4ex)[1n(x+m)-lnx]=0有两个不同的根,其中e为自然对数的底数,则实数a的取值范围是( )
| A. | (-∞,0) | B. | (0,$\frac{1}{2e}$) | C. | (-∞,0)∪($\frac{1}{2e}$,+∞) | D. | ($\frac{1}{2e}$,+∞) |
18.已知集合U={1,2,3,4,5,6},集合A={2,3},集合B={1,2,4},则(∁UB)∩A=( )
| A. | {2} | B. | {3} | C. | {5,6} | D. | {3,5,6} |
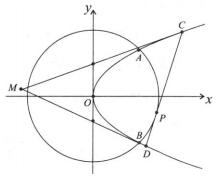 如图,已知抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.
如图,已知抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.