题目内容
11.若m=${∫}_{-1}^{1}$(6x2+tanx)dx,且(2x+$\sqrt{3}$)m=a0+a1x+a2x2+…+amxm,则(a0+a2+…+am)2-(a1+..+am-1)2的值为1.分析 m=${∫}_{-1}^{1}$(6x2+tanx)dx=$(2{x}^{3}){|}_{-1}^{1}$+${∫}_{-1}^{1}tanxdx$=4,可得$(2x+\sqrt{3})^{4}$=a0+a1x+a2x2+…+${a}_{4}{x}^{4}$,分别令x=1,x=-1,即可得出.
解答 解:m=${∫}_{-1}^{1}$(6x2+tanx)dx=$(2{x}^{3}){|}_{-1}^{1}$+${∫}_{-1}^{1}tanxdx$=4,
∴$(2x+\sqrt{3})^{4}$=a0+a1x+a2x2+…+${a}_{4}{x}^{4}$,
令x=1,则a0+a1+a2+a3+a4=$(2+\sqrt{3})^{4}$,
令x=-1,则a0-a1+a2-a3+a4=$(2-\sqrt{3})^{4}$,
则(a0+a2+a4)2-(a1+a3)2=(a0+a1+a2+a3+a4)(a0-a1+a2-a3+a4)=$(2+\sqrt{3})^{4}$$(2-\sqrt{3})^{4}$=1.
故答案为:1.
点评 本题考查了微积分基本定理、二项式定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.在区间$[{-\frac{5}{6},\frac{13}{6}}]$上随机取一个数x,则事件“$-1≤{log_{\frac{1}{3}}}({x+1})≤1$”不发生的概率为( )
| A. | $\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
16.设A是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点,F(c,0)是右焦点,若抛物线${y^2}=-\frac{{4{a^2}}}{c}x$的准线l上存在一点P,使∠APF=30°,则双曲线的离心率的范围是( )
| A. | [2,+∞) | B. | (1,2] | C. | (1,3] | D. | [3,+∞) |
20.设集合$A=\left\{{({x,y})|\frac{x^2}{4}+\frac{y^2}{16}=1}\right\}$,B={(x,y)|y=3x},则A∩B的子集的个数是( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
1.已知点P在抛物线y=x2上,点Q在圆(x-4)2+(y+$\frac{1}{2}$)2=1上,则|PQ|的最小值为( )
| A. | $\frac{3\sqrt{5}}{2}$-1 | B. | $\frac{3\sqrt{3}}{2}$-1 | C. | 2$\sqrt{3}$-1 | D. | $\sqrt{10}$-1 |
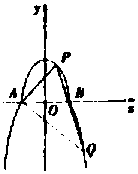 如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.
如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.