题目内容
6.已知函数f(x)=2lnx,g(x)=$\frac{1}{2}$ax2+(2a-1)x(Ⅰ)设h(x)=f(x)-g(x),讨论函数h(x)的单调区间;
(II )若f(x)-ax=0有两个不同实数解x1,x2,求证:lnx1+lnx2>2.
分析 (Ⅰ)先求导,再分类讨论,根据导数和函数的单调性即可求出,
(Ⅱ)f(x)-ax=0有两个不同实数解x1,x2,则f(x)的两个相异零点为x1,x2,设x2>x1>0,得到lnx1-ax1=0,lnx2-ax2=0,通过两式相减,整理化简可得ln$\frac{{x}_{2}}{{x}_{1}}$>$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}+{x}_{2}}$,然后换元,构造函数,根据导数和函数的最值即可证明
解答 解:(Ⅰ)h(x)=f(x)-g(x)=2lnx-$\frac{1}{2}$ax2-(2a-1)x,x>0,
∴h′(x)=$\frac{2}{x}$-ax-(2a-1)=-$\frac{(ax-1)(x+2)}{x}$,
①当a≤0时,h′(x)>0在(0,+∞)恒成立,
∴h(x)在(0,+∞)上单调递增,
②当a>0时,令h′(x)=0,解得x=$\frac{1}{a}$,
当0<x<$\frac{1}{a}$时,h′(x)>0,函数h(x)单调递增,
当x>$\frac{1}{a}$时,h′(x)<0,函数h(x)单调递减,
综上所述:当a≤0时,f(x)在(0,+∞)单调递增,
当a>0时,f(x)在(0,$\frac{1}{a}$)单调递增,在($\frac{1}{a}$,+∞)单调递减;
(Ⅱ)证明:f(x)-ax=0有两个不同实数解x1,x2,
则f(x)的两个相异零点为x1,x2,设x2>x1>0,
∵f(x1)=0,f(x2)=0,
∴lnx1-ax1=0,lnx2-ax2=0,
∴lnx1-lnx2=a(x1-x2),lnx1+lnx2=a(x1+x2),
∵x1x2>e2,
若lnx1+lnx2>2,
则a(x1+x2)>2,
即$\frac{ln{x}_{2}-ln{x}_{1}}{{x}_{2}-{x}_{1}}$>$\frac{2}{{x}_{1}+{x}_{2}}$a,即ln$\frac{{x}_{2}}{{x}_{1}}$>$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}+{x}_{2}}$,
不妨设设t=ln$\frac{{x}_{2}}{{x}_{1}}$>1,
构造函数h(t)=lnt-$\frac{2(t-1)}{1+t}$,
则h′(t)=$\frac{(t-1)^{2}}{t(t+1)^{2}}$>0,
∴h(t)在(1,+∞)上是增函数,
∴h(e)>h(1)=0,
∴lnt>$\frac{2(t-1)}{1+t}$,
∴lnx1+lnx2>2.
点评 本题考查导数的运用:单调区间、极值和最值,考查分类讨论思想方法和构造函数法,以及转化思想的运用,考查化简整理的运算能力,属于难题.

| A. | -$\frac{5}{3}$ | B. | -$\frac{1}{3}$ | C. | -1 | D. | -5 |
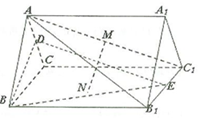 如图,正三棱柱ABC-A1B1C1中,侧棱$A{A_1}=\sqrt{3}$,AB=2,D,E分别为棱AC,B1C1的中点,M,N分别为线段AC1和BE的中点.
如图,正三棱柱ABC-A1B1C1中,侧棱$A{A_1}=\sqrt{3}$,AB=2,D,E分别为棱AC,B1C1的中点,M,N分别为线段AC1和BE的中点.