题目内容
15.已知向量$\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(-3,1)则下列结论正确的是( )| A. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$) | D. | $\overrightarrow{a}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$) |
分析 求出$\overrightarrow{a}$-$\overrightarrow{b}$,利用向量的数量积判断求解即可.
解答 解:向量$\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(-3,1),
显然$\overrightarrow{a}⊥\overrightarrow{b}$,不正确;$\overrightarrow{a}∥\overrightarrow{b}$也不正确;
$\overrightarrow{a}$+$\overrightarrow{b}$=(-4,3),$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=(-1,2)•(-4,3)=10≠0,所以C选项不正确;
$\overrightarrow{a}-\overrightarrow{b}$=(2,1),$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=-2+2=0.
∴$\overrightarrow{a}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$).
故选:D.
点评 本题考查向量的数量积的运算,向量的坐标运算,考查计算能力.

练习册系列答案
相关题目
3.已知复数z满足z(1+i)2=1-i,则复数z对应的点在( )上.
| A. | 直线y=-$\frac{1}{2}$x | B. | 直线y=$\frac{1}{2}$x | C. | 直线y=-$\frac{1}{2}$ | D. | 直线x=-$\frac{1}{2}$ |
10.若复数z=$\frac{a+i}{2i}$(a∈R,i为虚数单位)的实部与虚部相等,则z的模等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
7.已知函数f(x)是定义在R上的偶函数,若当x<0时,f(x)=-log2(-2x),则f(32)=( )
| A. | -32 | B. | -6 | C. | 6 | D. | 64 |
 如图,四棱锥P-ABCD中,∠BAD=∠ABC=90°,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为90°.
如图,四棱锥P-ABCD中,∠BAD=∠ABC=90°,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为90°.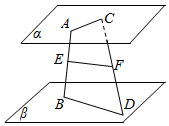 已知:如图,平面α、β满足α∥β,A、C∈α,B、D∈β,E∈AB,F∈CD,AC与BD异面,且$\frac{AE}{EB}=\frac{CF}{FD}$.求证:EF∥β
已知:如图,平面α、β满足α∥β,A、C∈α,B、D∈β,E∈AB,F∈CD,AC与BD异面,且$\frac{AE}{EB}=\frac{CF}{FD}$.求证:EF∥β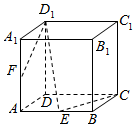 如图所示,在正方体AC1中,E,F分别是AB,AA1的中点.
如图所示,在正方体AC1中,E,F分别是AB,AA1的中点.