题目内容
在 中,边
中,边 、
、 、
、 分别是角
分别是角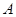 、
、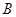 、
、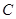 的对边,且满足
的对边,且满足 .
.
(1)求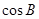 ;
;
(2)若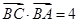 ,
,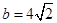 ,求边
,求边 ,
, 的值.
的值.
(1)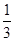 (2)
(2) 或
或 .
.
解析试题分析:(1)根据正弦定理把已知等式转化为角的三角函数式 ,然后再化简整理,可得
,然后再化简整理,可得 .即可得出
.即可得出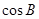 的值;(2)应用向量的数量积公式把
的值;(2)应用向量的数量积公式把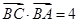 转化为关于边的等式,即
转化为关于边的等式,即 . ①;然后再利用余弦公式表示出
. ①;然后再利用余弦公式表示出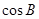 ,整理得到
,整理得到 . ②,解①和②组成的方程组,即可得到a,c的值.
. ②,解①和②组成的方程组,即可得到a,c的值.
试题解析:解:(1)由正弦定理和 ,得
,得 , 2分
, 2分
化简,得
即 , 4分
, 4分
故 .
.
所以 . 5分
. 5分
(2)因为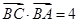 , 所以
, 所以
所以 ,即
,即 . (1) 7分
. (1) 7分
又因为 ,
,
整理得, . (2) 9分
. (2) 9分
联立(1)(2)  ,解得
,解得 或
或 . 10分
. 10分
考点:1.正弦定理和余弦定理;2.向量的数量积.

练习册系列答案
相关题目
 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 .设向量
.设向量 ,
, .
. ,
, ,求角
,求角 ,
,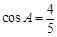 ,求
,求 的值.
的值.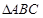 的内角A、B、C所对的边为
的内角A、B、C所对的边为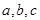 ,
,  ,
, 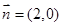 ,且
,且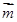 与
与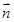 所成角为
所成角为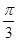 .
. 的取值范围.
的取值范围.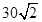 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于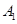 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西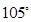 方向的
方向的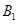 处,此时两船相距
处,此时两船相距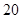 海里,当甲船航行
海里,当甲船航行 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西 方向的
方向的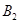 处,此时两船相距
处,此时两船相距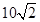 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?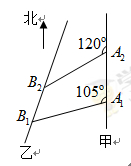
 ABC中,内角A,B,C的对边分别为a,b,c.
ABC中,内角A,B,C的对边分别为a,b,c. ,
, .
. 的值; (Ⅱ)若
的值; (Ⅱ)若 ,求
,求 ,已知石塔的高度为
,已知石塔的高度为 .
.
 为观测点,在塔顶
为观测点,在塔顶 处测得地面上一点
处测得地面上一点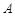 的俯角为
的俯角为 ,在塔底
,在塔底 处测得
处测得 ,用
,用 表示山的高度
表示山的高度 ;
; 上,其中
上,其中 是塔顶
是塔顶 ,当观测点
,当观测点 在
在 时看
时看 )最大,求山的高度
)最大,求山的高度 的内角
的内角 所对边的长分别为
所对边的长分别为 ,且有
,且有 .
.
 ,
, ,
, 为
为 的中点,求
的中点,求 的长.
的长. 中,内角
中,内角 对边分别为
对边分别为 ,
,
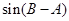 的值.
的值. 中,
中, ,
, ,设
,设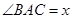 ,并记
,并记
 的解析式及其定义域;
的解析式及其定义域; ,若函数
,若函数 的值域为
的值域为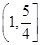 ,试求正实数
,试求正实数 的值
的值