题目内容
如图,山顶有一座石塔 ,已知石塔的高度为
,已知石塔的高度为 .
.
(Ⅰ)若以 为观测点,在塔顶
为观测点,在塔顶 处测得地面上一点
处测得地面上一点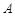 的俯角为
的俯角为 ,在塔底
,在塔底 处测得
处测得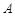 处的俯角为
处的俯角为 ,用
,用 表示山的高度
表示山的高度 ;
;
(Ⅱ)若将观测点选在地面的直线 上,其中
上,其中 是塔顶
是塔顶 在地面上的射影.已知石塔高度
在地面上的射影.已知石塔高度 ,当观测点
,当观测点 在
在 上满足
上满足 时看
时看 的视角(即
的视角(即 )最大,求山的高度
)最大,求山的高度 .
.
(Ⅰ) ; (Ⅱ)
; (Ⅱ)
解析试题分析:(Ⅰ)直接由正弦定理可得 ,从而
,从而 ,故
,故
 ,注意处理好俯角;(Ⅱ)设
,注意处理好俯角;(Ⅱ)设 ,根据当观测点
,根据当观测点 在
在 上满足
上满足 时看
时看 的视角(即
的视角(即 )最大可先求出
)最大可先求出
 ,然后由基本不等式求出
,然后由基本不等式求出
 及最值取到的条件
及最值取到的条件 得出
得出 .
.
试题解析:(Ⅰ)在△ 中,
中, ,
, ,
,
由正弦定理得:

则 =
= 4分
4分
(Ⅱ)设 ,
, ,
,
 6分
6分

当且仅当 即
即 时,
时, 最大,从而
最大,从而 最大,
最大,
由题意, ,解得
,解得 .
.
考点:1.正弦定理的应用;2.三角恒等变换;3.基本不等式的应用

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 ,函数
,函数 满足
满足 .
. 的单调递减区间;
的单调递减区间; 的内角
的内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且 , 求
, 求 的取值范围.
的取值范围. 两个小岛相距10
两个小岛相距10 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至 处进行作业,且
处进行作业,且 .设
.设

 分别表示
分别表示 和
和 ,并求出
,并求出 的距离为
的距离为 ,求BD的最大值.
,求BD的最大值.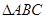 中,
中,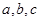 分别为内角A,B,C所对的边长,
分别为内角A,B,C所对的边长,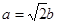 ,
,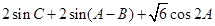
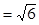 .
.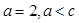 求
求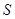 .
. 中,边
中,边 、
、 、
、 分别是角
分别是角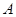 、
、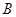 、
、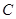 的对边,且满足
的对边,且满足 .
.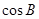 ;
;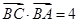 ,
,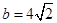 ,求边
,求边 内角
内角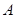 、
、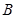 、
、 所对的边分别为
所对的边分别为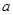 、
、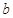 、
、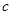 .已知
.已知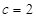 ,
,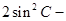
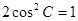 .
.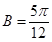 时,求
时,求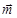 =(sinA,1),
=(sinA,1),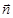 =(cosA,
=(cosA,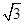 ),且
),且 ,求△ABC的面积.
,求△ABC的面积. 处下山至
处下山至 处有两条路径.一条是从
处有两条路径.一条是从 ,然后从
,然后从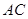 匀速步行,速度为
匀速步行,速度为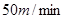 .在甲出发
.在甲出发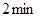 后,乙从
后,乙从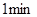 后,再从
后,再从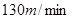 ,索道
,索道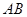 长为
长为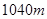 ,经测量
,经测量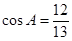 ,
,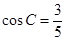 .
.
 分钟,乙步行的速度应控制在什么范围内?
分钟,乙步行的速度应控制在什么范围内? 是锐角三角形,
是锐角三角形, 分别是内角A,B,C所对边长,并且
分别是内角A,B,C所对边长,并且
 ,求
,求 (其中
(其中 ).
).