题目内容
20.执行如图所示的程序框图,则输出的结果是( )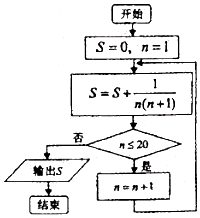
| A. | $\frac{21}{22}$ | B. | $\frac{20}{21}$ | C. | $\frac{19}{20}$ | D. | $\frac{22}{23}$ |
分析 由题意可知,该程序的作用是求解S=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{21×22}$的值,然后利用裂项求和即可求解
解答 解:由题意可知,该程序的作用是求解S=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{21×22}$的值,
而S=$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{21×22}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{21}$-$\frac{1}{22}$
=1-$\frac{1}{22}$=$\frac{21}{22}$
故选A.
点评 本题考查了程序框图中的循环结构的应用,解题的关键是由框图的结构判断出框图的计算功能.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知O,F分别为双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的中心和右焦点,点G、M分别在E的渐近线和右支上,若$\overrightarrow{FG}$•$\overrightarrow{OG}$=0,GM∥x轴,|OM|=|OF|,则E的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
8.若函数f(x)=2ax2-x-1在(0,1)内恰有一个零点,则实数a的取值范围是( )
| A. | (-1,1) | B. | [1,+∞) | C. | (1,+∞) | D. | (2,+∞) |
10.函数f(x)=logax(a>0,且a≠1)恒过定点( )
| A. | (0,1) | B. | (1,0) | C. | (1,1) | D. | (a,1) |