题目内容
6.求函数y=-x2+2ax(其中a为常数)在区间[-1,1]上的最小值.分析 求得二次函数的对称轴方程,对a讨论区间[-1,1]的位置关系,分当a≥1时,当a≤-1时,当-1<a≤0时,当0<a<1时,讨论单调性,即可得到所求最小值.
解答 解:函数y=-x2+2ax的图象为开口向下,对称轴为x=a,
①当a≥1时,区间[-1,1]为增区间,可得f(-1)取得最小值,且为-1-2a;
②当a≤-1时,区间[-1,1]为减区间,可得f(1)取得最小值,且为-1+2a;
③当-1<a≤0时,f(-1)≥f(1),可得[-1,a)递增,(a,1]递减,则f(1)=2a-1为最小值;
④当0<a<1时,f(-1)<f(1),可得[-1,a)递增,(a,1]递减,则f(-1)=-2a-1为最小值.
综上可得,当a>0时,f(x)的最小值为f(-1)=-1-2a;
当a≤0时,f(x)的最小值为f(1)=-1+2a.
点评 本题考查二次函数在闭区间上的最值的求法,注意运用对称轴和区间的关系,运用函数的单调性,考查运算能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
1.若函数f(x)为定义在R上的偶函数,其导函数为f′(x),对任意实数x满足xf′(x)>-f(-x),则不等式xf(x)<(1-2x)f(1-2x)的解集是( )
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,+∞) | C. | (-∞,$\frac{1}{3}$) | D. | (-∞,$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
15.下列函数中,在x=0处的导数不等于零的是( )
| A. | y=x3+x2 | B. | y=x+e-x | C. | y=(x-1)e2 | D. | y=xsinx |
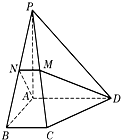 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,M、N分别为PC、PB的中点.PA=AB.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,M、N分别为PC、PB的中点.PA=AB.