题目内容
2.用与球心距离为1的平面去截球,所得截面圆的面积为π,则球的表面积为( )| A. | $\frac{8π}{3}$ | B. | $\frac{32π}{3}$ | C. | 8π | D. | $\frac{8\sqrt{2}π}{3}$ |
分析 求出截面圆的半径为$\sqrt{{R}^{2}-1}$,利用截面圆的面积为π,可得R2=2,即可求出球的表面积.
解答 解:设半径为R,则截面圆的半径为$\sqrt{{R}^{2}-1}$,
∴截面圆的面积为S=(R2-1)π=π,∴R2=2,
∴球的表面积S=4πR2=8π.
故选C.
点评 本题考查球的表面积,考查勾股定理的运用,比较基础.

练习册系列答案
相关题目
17.若函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R)有极值点,则导函数f′(x)的图象可能是( )
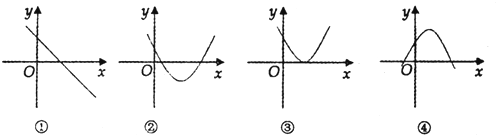

| A. | ①③ | B. | ②③ | C. | ①②④ | D. | ②④ |
7.已知函数f(x)=-$\frac{1}{3}$x3+x2+ax+b在x=3取得极值为4,则f(x)在区间[-2,1]上的最大值为( )
| A. | -1 | B. | 0 | C. | -$\frac{4}{3}$ | D. | -$\frac{13}{3}$ |
14.直线l与抛物线y2=8x交于A、B两点,若线段AB中点的纵坐标为2,则l的斜率等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=1,点M是SD的重点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB=1,点M是SD的重点,AN⊥SC,且交SC于点N.