题目内容
5.设函数f(x)=x3-4x-a,0<a<2.若f(x)的三个零点为x1,x2,x3,且x1<x2<x3,则( )| A. | x1<-2 | B. | x2>0 | C. | x3<1 | D. | x3>2 |
分析 利用导数研究函数的单调性,利用导数求函数的极值,再根据f (x)的三个零点为x1,x2,x3,且x1<x2<x3,求得各个零点所在的区间,从而得出结论.
解答 解:∵函数f (x)=x3-4x+a,0<a<2,∴f′(x)=3x2-4.
令f′(x)=0,可得 x=±$\frac{2\sqrt{3}}{3}$.
∵当x<-$\frac{2\sqrt{3}}{3}$时,f′(x)>0;在(-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$)上,f′(x)<0;
在($\frac{2\sqrt{3}}{3}$,+∞)上,f′(x)>0.
故函数在(-∞,-$\frac{2\sqrt{3}}{3}$)上是增函数,在(-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$)上是减函数,在($\frac{2\sqrt{3}}{3}$,+∞)上是增函数.
故f(-$\frac{2\sqrt{3}}{3}$)是极大值,f($\frac{2\sqrt{3}}{3}$)是极小值.
再由f(x)的三个零点为x1,x2,x3,且x1<x2<x3,可得 x1<-$\frac{2\sqrt{3}}{3}$,-$\frac{2\sqrt{3}}{3}$<x2<$\frac{2\sqrt{3}}{3}$,x3>$\frac{2\sqrt{3}}{3}$.
根据f(0)=a>0,且f($\frac{2\sqrt{3}}{3}$)=a-$\frac{16\sqrt{3}}{9}$<0,可得 $\frac{2\sqrt{3}}{3}$>x2>0,
故选:B.
点评 本题主要考查函数的零点的定义,函数的零点与方程的根的关系,利用导数研究函数的单调性,利用导数求函数的极值,属于中档题.

 学业测评一课一测系列答案
学业测评一课一测系列答案| A. | [-6,-2] | B. | $[-6,-\frac{9}{8}]$ | C. | [-5,-3] | D. | [-4,-3] |
2
4 6 8
10 12 14 16 18
20 22 24 26 28 30 32
…
| A. | 654 | B. | 656 | C. | 658 | D. | 660 |
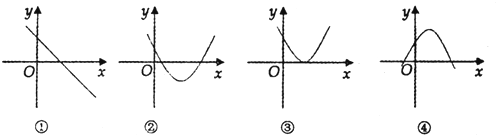
| A. | ①③ | B. | ②③ | C. | ①②④ | D. | ②④ |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | f(k)+$\frac{1}{3(k+1)+1}$ | B. | f(k)+$\frac{2}{3k+2}$ | ||
| C. | f(k)+$\frac{1}{3k+2}$+$\frac{1}{3k+3}$+$\frac{1}{3k+4}$-$\frac{1}{k+1}$ | D. | f(k)+$\frac{1}{3k+4}$-$\frac{1}{k+1}$ |