题目内容
12.椭圆的两焦点分别为F1(-4,0),F2(4,0),过F1作弦AB,且△ABF2的周长为20,则此椭圆的方程为$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1.分析 由题意可设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0).根据过F1作弦AB,且△ABF2的周长为20,则4a=20,解得a,又c=4,则$b=\sqrt{{a}^{2}-{c}^{2}}$,即可得出.
解答 解:由题意可设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0).
∵过F1作弦AB,且△ABF2的周长为20,则4a=20,解得a=5,
又c=4,则$b=\sqrt{{a}^{2}-{c}^{2}}$=3.
∴椭圆的标准方程为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1.
故答案为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1.
点评 本题考查了椭圆的定义标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2. 如图给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为${a_{ij}}(i≥j,i,j∈{N^*})$,则a63=( )
如图给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为${a_{ij}}(i≥j,i,j∈{N^*})$,则a63=( )
 如图给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为${a_{ij}}(i≥j,i,j∈{N^*})$,则a63=( )
如图给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为${a_{ij}}(i≥j,i,j∈{N^*})$,则a63=( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
20.将正偶数按下边规律排列,第19行,从左到右,第6个数是( )
2
4 6 8
10 12 14 16 18
20 22 24 26 28 30 32
…
2
4 6 8
10 12 14 16 18
20 22 24 26 28 30 32
…
| A. | 654 | B. | 656 | C. | 658 | D. | 660 |
17.若函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R)有极值点,则导函数f′(x)的图象可能是( )
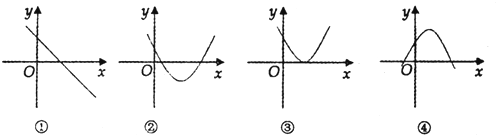

| A. | ①③ | B. | ②③ | C. | ①②④ | D. | ②④ |