题目内容
7.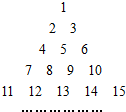 将全体正整数排成一个三角形数阵:按照如图所示排列的规律:
将全体正整数排成一个三角形数阵:按照如图所示排列的规律:(1)第7行从左到右的第3个数为24.
(2)第n行(n≥3)从左向右的第3个数为$\frac{{n}^{2}-n+6}{2}$.
分析 先找到数的分布规律,求出第n-1行结束的时候一共出现的数的个数,再求第n行从左向右的第3个数,代入n=7可得.
解答 解:由排列的规律可得,第n-1行结束的时候共排了1+2+3+…+(n-1)=$\frac{(n-1)n}{2}$个数,
∴第n行从左向右的第3个数为$\frac{(n-1)n}{2}$+3=$\frac{{n}^{2}-n+6}{2}$,
把n=7代入可得第7行从左向右的第3个数为24,
故答案为:24,$\frac{{n}^{2}-n+6}{2}$.
点评 本题借助于一个三角形数阵考查等差数列的应用,考查归纳推理,属基础题.

练习册系列答案
相关题目
17.若函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R)有极值点,则导函数f′(x)的图象可能是( )
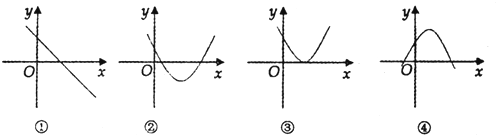

| A. | ①③ | B. | ②③ | C. | ①②④ | D. | ②④ |
15.已知f(n)=$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{3n+1}$,则f(k+1)等于( )
| A. | f(k)+$\frac{1}{3(k+1)+1}$ | B. | f(k)+$\frac{2}{3k+2}$ | ||
| C. | f(k)+$\frac{1}{3k+2}$+$\frac{1}{3k+3}$+$\frac{1}{3k+4}$-$\frac{1}{k+1}$ | D. | f(k)+$\frac{1}{3k+4}$-$\frac{1}{k+1}$ |
19.过点A(3,1)作圆(x-2)2+(y-2)2=4的弦,则当弦长最短时弦所在的直线方程为( )
| A. | x+y-4=0 | B. | x-y+2=0 | C. | x+y+4=0 | D. | x-y-2=0 |