题目内容
设A(xA,yA),B(xB,yB)为平面直角坐标系上的两点,其中xA,yA,xB,yB∈Z.令△x=xB-xA,△y=yB-yA,若|△x|+|△y|=3,且|△x|•|△y|≠0,则称点B为点A的“相关点”,记作:B=τ(A),已知P0(x0,y0),(x0,y0∈Z)为平面上一个定点,平面上点列{Pi}满足:Pi=τ(Pi-1),且点Pi的坐标为(xi,yi),其中i=1,2,3,…,n,则点P0的“相关点”有( )个.
| A、4 | B、6 | C、8 | D、10 |
考点:进行简单的合情推理
专题:计算题,新定义
分析:根据绝对值的意义,可得整数△x与△y在{±1,±2}中取值,满足绝对值的和等于3,由此可得点P0的相关点有8个
解答:
解:∵|△x|+|△y|=3,(|△x|•|△y|≠0)
∴|△x|=1且|△y|=2,或|△x|=2且|△y|=1,
∴点P0的相关点有8个.
故选:C.
∴|△x|=1且|△y|=2,或|△x|=2且|△y|=1,
∴点P0的相关点有8个.
故选:C.
点评:本题给出平面坐标系内“相关点”的定义,考查绝对值的意义,考查学生对新定义的理解,属于基础题.

练习册系列答案
相关题目
下列命题中,真命题是( )
| A、?x0∈R,|x0|≤0 | ||
| B、?x∈R,2x>x2 | ||
C、a-b=0的充要条件是
| ||
| D、若p∧q为假,则p∨q为假(p,q是两个命题) |
已知a,b,c是三条不同的直线,α,β,γ是三个不同的平面,上述命题中真命题的是( )
| A、若a⊥c,b⊥c,则a∥b或a⊥b |
| B、若α⊥β,β⊥γ,则α∥β |
| C、若a?α,b?β,c?β,a⊥b,a⊥c,则α⊥β; |
| D、若a⊥α,b?β,a∥b,则α⊥β |
执行如图所示的程序框图,输出的k值为( )


| A、3 | B、4 | C、5 | D、6 |
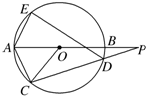 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,求证:∠PDE=∠POC.
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,求证:∠PDE=∠POC.