题目内容
2.若变量x,y满足条件$\left\{\begin{array}{l}3x-y≤0\\ x-3y+5≥0\\ x≥0\end{array}\right.$则z=x+y的最大值为( )| A. | 0 | B. | $\frac{5}{3}$ | C. | 2 | D. | $\frac{5}{2}$ |
分析 画出约束条件的可行域,利用目标函数的几何意义求解即可.
解答 解:由约束条件$\left\{\begin{array}{l}3x-y≤0\\ x-3y+5≥0\\ x≥0\end{array}\right.$作出可行域如图,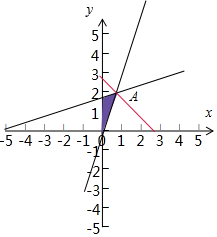
由$\left\{\begin{array}{l}{3x-y=0}\\{x-3y+5=0}\end{array}\right.$可知,A($\frac{5}{8}$,$\frac{15}{8}$).
化目标函数z=x+y为y=-x+z,
由图可知,当直线y=-x+z过A时,直线在y轴上的截距最大,z有最大值为$\frac{5}{2}$.
故选:D.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
12.对于满足0<b<3a的任意实数a,b,函数f(x)=ax2+bx+c总有两个不同的零点,则$\frac{a+b-c}{a}$的取值范围是( )
| A. | $({1,\frac{7}{4}}]$ | B. | (1,2] | C. | [1,+∞) | D. | (2,+∞) |
11.某机构通过对某企业2016年的生产经营情况的调查,得到每月利润y(单位:万元)与相应月份数x的部分数据如表:
(1)根据如表数据,请从下列三个函数中选取一个恰当的函数描述y与x的变化关系,并说明理由,y=ax3+b,y=-x2+ax+b,y=a•bx.
(2)利用(1)中选择的函数,估计月利润最大的是第几个月,并求出该月的利润.
| x | 1 | 4 | 7 | 12 |
| y | 229 | 244 | 241 | 196 |
(2)利用(1)中选择的函数,估计月利润最大的是第几个月,并求出该月的利润.
