题目内容
10.下列结论:①一次试验中不同的基本事件不可能同时发生;
②设k<3,k≠0,则$\frac{x^2}{3-k}-\frac{y^2}{k}=1$与$\frac{x^2}{5}+\frac{y^2}{2}=1$必有相同的焦点;
③点P(m,3)在圆(x-2)2+(y-1)2=2的外部;
④已知ab<0,bc<0,则直线ax+by-c=0通过第一、三、四象限.
其中正确的序号是②③④.
分析 ①,基本事件的特点是任意两个基本事件是互斥的;
②,设k<3,k≠0,当0<k<3,则0<3-k<3,$\frac{x^2}{3-k}-\frac{y^2}{k}=1$表实轴为x轴的双曲线,a2+b2=3=c2.
当k<0时,-k>0,且3-k>-k,$\frac{x^2}{3-k}-\frac{y^2}{k}=1$表实轴为x轴焦点在x轴上的椭圆.a2=3-k,b2=-k.
③,(m-2)2+(3-1)2>2,可判定
④把直线的方程化为斜截式,判断斜率及在y轴上的截距的符号,从而确定直线在坐标系中的位置
解答 解:对于①,∵基本事件的特点是任意两个基本事件是互斥的,∴一次试验中,不同的基本事件不可能同时发生.故正确
对于②,设k<3,k≠0,当0<k<3,则0<3-k<3,$\frac{x^2}{3-k}-\frac{y^2}{k}=1$表实轴为x轴的双曲线,a2+b2=3=c2.
∴二曲线有相同焦点;当k<0时,-k>0,且3-k>-k,$\frac{x^2}{3-k}-\frac{y^2}{k}=1$表实轴为x轴焦点在x轴上的椭圆.a2=3-k,b2=-k.
∴a2-b2=3=c2与已知椭圆有相同焦点.故正确;
对于③,∵(m-2)2+(3-1)2>2,∴点P(m,3)在圆(x-2)2+(y-1)2=2的外部,故正确;
对于④,由ab<0,bc<0得,则直线ax+by-c=0的斜率k>0,直线在y轴上的截距为$\frac{c}{b}<0$,故直线第一、三、四象限,正确.
故答案为:②③④
点评 本题考查了命题真假的判定,涉及了大量的基础知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.调查某高中1000名学生的肥胖情况,得下表:
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15
(Ⅰ)求x的值;
(Ⅱ)已知y≥195,z≥195,求肥胖学生中男生不少于女生的概率.
| 偏瘦 | 正常 | 肥胖 | |
| 女生(人) | 100 | 173 | y |
| 男生(人) | x | 177 | z |
(Ⅰ)求x的值;
(Ⅱ)已知y≥195,z≥195,求肥胖学生中男生不少于女生的概率.
2.若变量x,y满足条件$\left\{\begin{array}{l}3x-y≤0\\ x-3y+5≥0\\ x≥0\end{array}\right.$则z=x+y的最大值为( )
| A. | 0 | B. | $\frac{5}{3}$ | C. | 2 | D. | $\frac{5}{2}$ |
20.某高中共有2000名学生,其中各年级男生、女生的人数如表所示,已知在全校学生中随机抽取1人,抽到高二年级女生的概率是0.19,现用分层抽样的方法在全校抽取64名学生,则在高三年级中应抽取的学生人数是( )
| 高一 | 高二 | 高三 | |
| 女生 | 373 | m | n |
| 男生 | 377 | 370 | p |
| A. | 8 | B. | 16 | C. | 28 | D. | 32 |
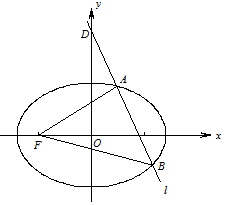 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,短轴端点与椭圆的两个焦点所构成的三角形面积为1,过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,短轴端点与椭圆的两个焦点所构成的三角形面积为1,过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.