题目内容
13.已知直线l经过直线3x+4y-2=0与直线x-y+4=0的交点P,且垂直于直线x-2y-1=0(Ⅰ)求直线l的方程
(Ⅱ)直线l与曲线y2+2x=0交于A,B两点,求|AB|
分析 (Ⅰ)求出P的坐标,利用直线l垂直于直线x-2y-1=0求直线l的方程
(Ⅱ)直线l与曲线y2+2x=0交于A,B两点,求出A,B的坐标,即可求|AB|.
解答 解:(Ⅰ)直线l经过直线3x+4y-2=0与直线x-y+4=0的交点P,可得P(-2,2),
∵直线l垂直于直线x-2y-1=0,
∴kl=-2,
∴直线l的方程为2x+y+2=0;
(Ⅱ)直线l与曲线y2+2x=0联立,可得y2-y-2=0,
∴y=-1或2,
∴A(-$\frac{1}{2}$,-1),B(-2,2)
∴|AB|=$\sqrt{(-2+\frac{1}{2})^{2}+(2+1)^{2}}$=$\frac{3\sqrt{5}}{2}$.
点评 本题考查直线方程,考查直线与直线,直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
3.曲线y=$\frac{x}{2x-1}$在点(1,1)处的切线方程为( )
| A. | x-y-2=0 | B. | x+y-2=0 | C. | x+4y-5=0 | D. | x-4y-5=0 |
1.调查某高中1000名学生的肥胖情况,得下表:
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15
(Ⅰ)求x的值;
(Ⅱ)已知y≥195,z≥195,求肥胖学生中男生不少于女生的概率.
| 偏瘦 | 正常 | 肥胖 | |
| 女生(人) | 100 | 173 | y |
| 男生(人) | x | 177 | z |
(Ⅰ)求x的值;
(Ⅱ)已知y≥195,z≥195,求肥胖学生中男生不少于女生的概率.
8.设点P(x,y)在椭圆4x2+y2=4上,则x+y的最大值为( )
| A. | 3 | B. | -3 | C. | 4 | D. | $\sqrt{5}$ |
2.若变量x,y满足条件$\left\{\begin{array}{l}3x-y≤0\\ x-3y+5≥0\\ x≥0\end{array}\right.$则z=x+y的最大值为( )
| A. | 0 | B. | $\frac{5}{3}$ | C. | 2 | D. | $\frac{5}{2}$ |
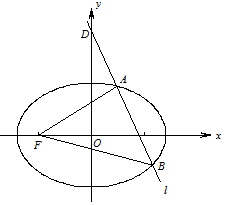 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,短轴端点与椭圆的两个焦点所构成的三角形面积为1,过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,短轴端点与椭圆的两个焦点所构成的三角形面积为1,过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.