题目内容
10.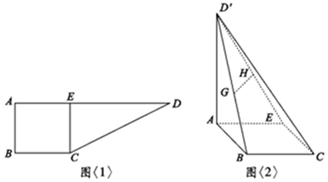 如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,如图<2>:若G,H分别为D′B,D′E的中点.
如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,如图<2>:若G,H分别为D′B,D′E的中点.(1)求证:GH⊥平面AD′C;
(2)求平面D′AB与平面D′CE的夹角.
分析 (1)证明BE⊥面ACD′,GH∥BE,即可得到GH⊥平面AD′C.
(2)如图过点D′作直线m∥AB,由AB∥EC,得直线m就是面D′AB与平面D′CE的交线,可得∠AD′E就是平面D′AB与平面D′CE的夹角的平面角,
解答 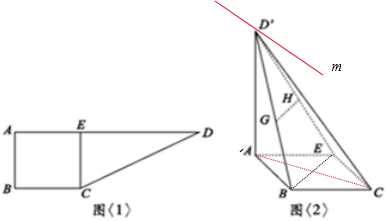 证明:(1)∵在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,
证明:(1)∵在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,
把△DEC沿CE折到D′EC的位置,使D′A=2$\sqrt{3}$,
∴AE=CE=2,D′E=6-2=4,∴D′A2+AE2=D′E2,CD′=$\sqrt{{2}^{2}+{4}^{2}}$=$2\sqrt{5}$,
∴AD′⊥AE,∵AD′⊥AB,AD′∩AB=A,∴AD′⊥平面ABCE,∴面AD′C⊥ABCE,又因为ABCE是正方形,∴BE⊥AC,
⇒BE⊥面ACD′,∵G,H分别为D′B,D′E的中点,∴GH∥BE,∴GH⊥平面AD′C;
(2)如图过点D′作直线m∥AB,∵AB∥EC,∴直线m就是面D′AB与平面D′CE的交线,
∵CE⊥AE,面AED′⊥面ABCE于AE,∴CE⊥D′E,即D′E⊥m,
∵AD′⊥AB,∴AD′⊥m,∵AD′?面AD′B,D′E?D′CE,∴∠AD′E就是平面D′AB与平面D′CE的夹角的平面角,
在直角三角形AD′E中,AE=2,D′E=4,可得,∴∠AD′E=30°.
平面D′AB与平面D′CE的夹角为300
点评 本题考查了空间线面垂直的判定,及定义法求二面角,属于中档题.

练习册系列答案
相关题目
4.已知实数x、y满足约束条件$\left\{\begin{array}{l}{y≥1-2x}\\{y<1+x}\\{x≤2}\end{array}\right.$,则目标函数z=x+y取不到的值是( )
| A. | 1 | B. | 3 | C. | 7 | D. | 4 |
18.已知实数a,b满足0<a<1,-1<b<1,则函数y=$\frac{1}{3}$ax3+ax2+b有三个零点的概率为( )
| A. | $\frac{5}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{11}{16}$ |
15.定义在R上的函数f(x)的导函数为f'(x),f(0)=0若对任意x∈R,都有f(x)>f'(x)+1,则使得f(x)+ex<1成立的x的取值范围为( )
| A. | (0,+∞) | B. | (-∞,0) | C. | (-1,+∞) | D. | (-∞,1) |
2.已知函数y=2|x|-4的图象与曲线C:x2+λy2=4恰有两个不同的公共点,则实数λ的取值范围是( )
| A. | [-$\frac{1}{4}$,$\frac{1}{4}$) | B. | [-$\frac{1}{4}$,$\frac{1}{4}$] | C. | (-∞,-$\frac{1}{4}$]∪(0,$\frac{1}{4}$) | D. | (-∞,-$\frac{1}{4}$]∪[$\frac{1}{4}$,+∞) |
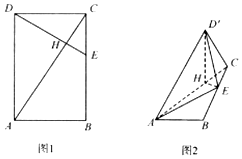 如图1,已知矩形ABCD中,$AB=2,BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.
如图1,已知矩形ABCD中,$AB=2,BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.