题目内容
15．定义在R上的函数f（x）的导函数为f'（x），f（0）=0若对任意x∈R，都有f（x）＞f'（x）+1，则使得f（x）+ex＜1成立的x的取值范围为（ ）| A． | （0，+∞） | B． | （-∞，0） | C． | （-1，+∞） | D． | （-∞，1） |
分析 构造函数：g（x）=$\frac{f（x）-1}{{e}^{x}}$，g（0）=$\frac{0-1}{{e}^{0}}$=-1．对任意x∈R，都有f（x）＞f'（x）+1，可得g′（x）=$\frac{{f}^{′}（x）+1-f（x）}{{e}^{x}}$＜0，函数g（x）在R单调递减，利用其单调性即可得出．
解答 解：构造函数：g（x）=$\frac{f（x）-1}{{e}^{x}}$，g（0）=$\frac{0-1}{{e}^{0}}$=-1．
∵对任意x∈R，都有f（x）＞f'（x）+1，
∴g′（x）=$\frac{{f}^{′}（x）{e}^{x}-[f（x）-1]{e}^{x}}{（{e}^{x}）^{2}}$=$\frac{{f}^{′}（x）+1-f（x）}{{e}^{x}}$＜0，
∴函数g（x）在R单调递减，
由f（x）+ex＜1化为：g（x）=$\frac{f（x）-1}{{e}^{x}}$＜-1=g（0），
∴x＞0．
∴使得f（x）+ex＜1成立的x的取值范围为（0，+∞）．
故选：A．
点评 本题考查了构造函数法、利用导数研究函数的单调性极值与最值、不等式的解法，考查了推理能力与计算能力，属于难题．
练习册系列答案
相关题目
9．当$\frac{2}{3}$＜m＜1时，复数z=（3m-2）+（m-1）i在复平面上对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
已知三棱柱ABC-A1B1C1的侧棱与底面ABC垂直，且AA1=4，AC=BC=2，∠ACB=90°．
3．已知双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点为A，抛物线C：y2=8ax的焦点为F，若在E的渐近线上存在点P使得PA⊥FP，则E的离心率的取值范围是（ ）
| A． | （1，2） | B． | （1，$\frac{3\sqrt{2}}{4}$] | C． | （2，+∞） | D． | [$\frac{3\sqrt{2}}{4}$，+∞） |
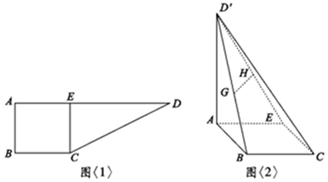如图＜1＞：在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC=2，AD=6，CE⊥AD于E点，把△DEC沿CE折到D′EC的位置，使D′A=2$\sqrt{3}$，如图＜2＞：若G，H分别为D′B，D′E的中点．