题目内容
已知函数f(x)=
是奇函数.
(1)求实数m的值;
(2)若函数f(x)在区间[-1,a-2]上单调递增,求实数a的取值范围;
(3)若函数f(x)=k有三个不同的实根,求实数k的取值范围.
|
(1)求实数m的值;
(2)若函数f(x)在区间[-1,a-2]上单调递增,求实数a的取值范围;
(3)若函数f(x)=k有三个不同的实根,求实数k的取值范围.
考点:根的存在性及根的个数判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)由函数f(x)=
是奇函数,满足f(-x)=-f(x),可求出实数m的值;
(2)根据(1)求出函数的解析式,分析函数的单调性,结合函数f(x)在区间[-1,a-2]上单调递增,构造关于a的不等式,解不等式可得实数a的取值范围;
(3)若方程f(x)=k有三个不同的实根,则函数f(x)的图象与直线y=k有三个不同的交点,数形结合易得答案.
|
(2)根据(1)求出函数的解析式,分析函数的单调性,结合函数f(x)在区间[-1,a-2]上单调递增,构造关于a的不等式,解不等式可得实数a的取值范围;
(3)若方程f(x)=k有三个不同的实根,则函数f(x)的图象与直线y=k有三个不同的交点,数形结合易得答案.
解答:
解:(1)∵函数f(x)=
是奇函数,满足f(-x)=-f(x),
不妨令x=1,则f(-1)=-f(1),
即1-m=-(-1+2),
解得m=2,
经检验f(x)=
,满足f(-x)=-f(x),
故m=2,
(2)函数f(x)=
的图象如下图所示:
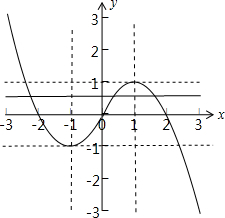
由图可知:函数f(x)的单调递增区间为[-1,1],
若函数f(x)在区间[-1,a-2]上单调递增,
则-1<a-2≤1,
解得a∈(1,3],
故实数a的取值范围为(1,3];
(3)若方程f(x)=k有三个不同的实根,
则函数f(x)的图象与直线y=k有三个不同的交点,
由(2)中图象可得:k∈(-1,1),
故实数k的取值范围为:(-1,1).
|
不妨令x=1,则f(-1)=-f(1),
即1-m=-(-1+2),
解得m=2,
经检验f(x)=
|
故m=2,
(2)函数f(x)=
|
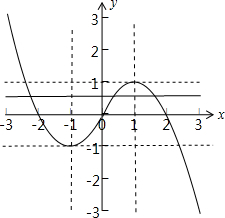
由图可知:函数f(x)的单调递增区间为[-1,1],
若函数f(x)在区间[-1,a-2]上单调递增,
则-1<a-2≤1,
解得a∈(1,3],
故实数a的取值范围为(1,3];
(3)若方程f(x)=k有三个不同的实根,
则函数f(x)的图象与直线y=k有三个不同的交点,
由(2)中图象可得:k∈(-1,1),
故实数k的取值范围为:(-1,1).
点评:本题考查函数单调性与奇偶性的结合,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数f(x)满足对任意的m,n∈Z+都有f(m+n)=f(m)•f(n)且f(1)=2,则
+
+…+
( )
| f(2) |
| f(1) |
| f(3) |
| f(2) |
| f(2011) |
| f(2010) |
| A、2011 | B、2010 |
| C、4020 | D、4022 |
设双曲线C:
-
=1(a>0,b>0)的离心率e=
,则该双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 4 |
| A、4x±3y=0 |
| B、3x±4y=0 |
| C、5x±3y=0 |
| D、3x±5y=0 |