题目内容
如图是求1×2+2×3+3×4+…+100×101的值的程序框图,则判断框内填写 .
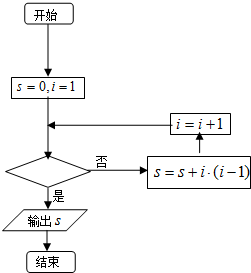

考点:程序框图
专题:算法和程序框图
分析:根据已知中的程序框图及程序功能,分析出循环变量i的终值应为101,故当i>101(i≥102)时,应结束循环,进而得到答案.
解答:
解:由已知中的程序功能是如图是求1×2+2×3+3×4+…+100×101的值,
由循环变量的初值为1,步长为1,
由S=S+i(i-1)得:循环变量i的终值应为101,
故当i>101(i≥102)时,应结束循环,
故判断框内应填写:i>101(i≥102),
故答案为:i>101(i≥102)
由循环变量的初值为1,步长为1,
由S=S+i(i-1)得:循环变量i的终值应为101,
故当i>101(i≥102)时,应结束循环,
故判断框内应填写:i>101(i≥102),
故答案为:i>101(i≥102)
点评:本题考查的知识点是程序框图,其中根据程序功能分析出循环变量的终值,是解答的关键.

练习册系列答案
相关题目
设正项等比数列{an}的前n项和为Sn,且210S30+S10=(210+1)S20,则数列{an}的公比为( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=sinx-x,则下列错误的是( )
| A、f(x)为奇函数 |
| B、f(x)在R上单调递减 |
| C、f(x)在R上无极值点 |
| D、f(x)在R上有三个零点 |