题目内容
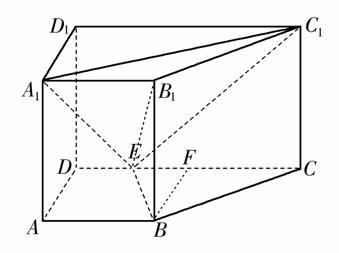
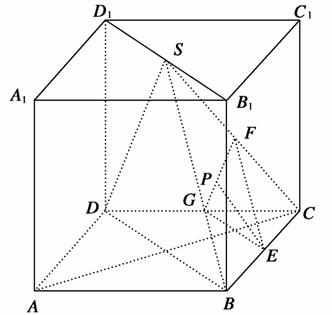
如图,直四棱柱ABCD-A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD=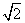 ,AA1=3,E为CD上一点,DE=1,EC=3.
,AA1=3,E为CD上一点,DE=1,EC=3.
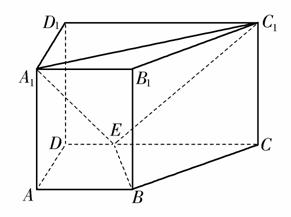
(1)证明:BE⊥平面BB1C1C;
(2)求点B1 到平面EA1C1 的距离.
[解析] (1)证明:过B作CD的垂线交CD于F,则
BF=AD=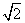 ,EF=AB-DE=1,FC=2.
,EF=AB-DE=1,FC=2.
在Rt△BFE中,BE=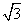 .
.
在Rt△CFB中,BC=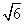 .
.
在△BEC中,因为BE2+BC2=9=EC2,故BE⊥BC.
由BB1⊥平面ABCD得BE⊥BB1,
所以BE⊥平面BB1C1C.
(2)连接B1E,则三棱锥E-A1B1C1的体积V=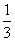 AA1·S△A1B1C1=
AA1·S△A1B1C1=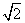 .
.
在Rt△A1D1C1中,A1C1=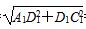 =3
=3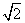 .
.
同理,EC1=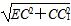 =3
=3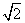 .
.
A1E=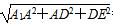 =2
=2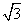 ,
,
故S△A1C1E=3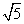 .
.
设点B1到平面EA1C1的距离为d,
则三棱锥B1-A1C1E的体积
V=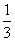 ·d·S△A1C1E=
·d·S△A1C1E=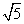 d,
d,
从而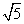 d=
d=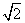 ,d=
,d=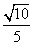 .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
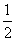 B.
B.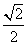
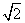
 π B.24-
π B.24-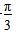

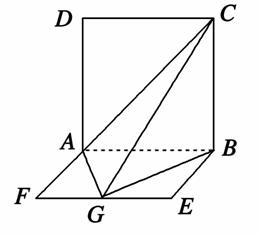
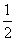 AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为________.
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为________.