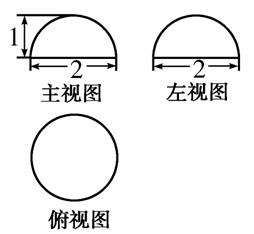
题目内容
在正方体ABCD－A1B1C1D1中，S是B1D1的中点，E、F、G分别是BC、SC和DC的中点，点P在线段FG上．
(1)求证：平面EFG∥平面SDB；
(2)求证：PE⊥AC.
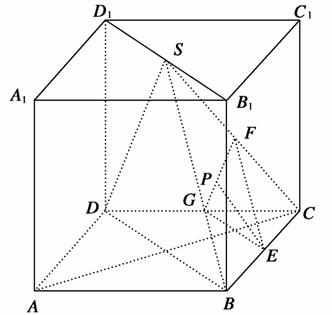
[解析] (1)∵E、F、G分别为BC、SC、CD的中点，
∴EF∥SB，EG∥BD.
∵EF平面SBD，EG平面SBD，
∴EF∥平面SBD，EG∥平面SBD.
∵EG∩EF＝E，∴平面EFG∥平面SDB.
(2)∵B1B⊥底面ABCD，∴AC⊥B1B.
又∵四边形ABCD是正方形，∴AC⊥BD.
∴AC⊥平面B1BDD1，即AC⊥平面SBD.
又平面EFG∥平面SBD，∴AC⊥平面EFG.
∵PE平面EFG，∴PE⊥AC.
练习册系列答案
阅读快车系列答案
相关题目
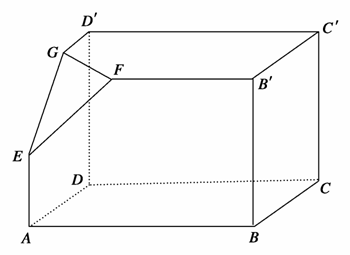
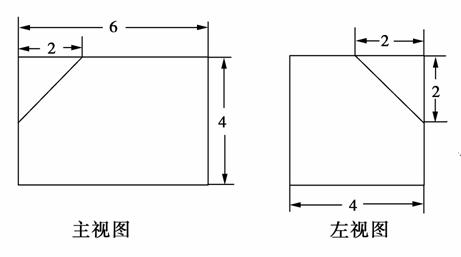
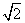，AA1＝3，E为CD上一点，DE＝1，EC＝3.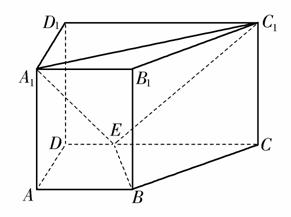
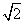，则此球的体积为( )
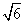π B．4
π