题目内容
8.设函数f(x)=ex-x-2(Ⅰ)求f(x)的单调区间;
(Ⅱ)当x∈[-3,2]时,求函数的最值.
分析 (Ⅰ)求出函数的导数,利用导函数的符号求解函数的单调区间.
(Ⅱ)求出函数的极小值端点函数值,即可得到函数的最值.
解答 解:(Ⅰ)f′(x)=ex-1,…(2分)
令f′(x)=ex-1>0,可得ex>1,解得x>0.
令f′(x)=ex-1<0,解得x<0.
∴f(x)的单调增区间:(0,+∞),单调减区间为:(-∞,0)…(6分)
(Ⅱ)由(Ⅰ)可知f(x)的单调增区间:(0,+∞),单调减区间为:(-∞,0).
x=0时,函数取得极小值.极小值为:f(0)=e0-0-2=-1,
f(-3)=e-3+1,f(2)=e2-4.
比较可知,当x∈[-3,2]时,函数的最大值e2-4.最小值为:-1.…(12分)
点评 本题考查函数的导数以及极值单调区间的求法,函数的最值的求法,考查分析问题解决问题的能力.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
19.若复数z满足(1-i)z=i,则复数z的模为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
16.设集合A={x|x2-2x=0},B={x|x2+2x=0},则A∪B=( )
| A. | {0} | B. | {0,2} | C. | {0,-2} | D. | {2,0,-2} |
3.下列结论①(sinx)′=-cosx;②$(\frac{1}{x})'=\frac{1}{x^2}$;③$({log_3}x)'=\frac{1}{3lnx}$;④$({x^2})'=\frac{1}{x}$.其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
13.化简$\frac{{tan{{22}°}+tan{{23}°}}}{{1-tan{{22}°}tan{{23}°}}}$得( )
| A. | -1 | B. | $\frac{π}{4}$ | C. | 1 | D. | 2 |
17.函数f(x)=2x+3x-7的零点所在的区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
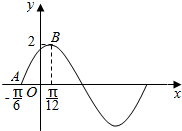 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示