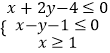题目内容
【题目】已知曲线C1的参数方程是 
（φ为参数），以坐标原点为极点，x轴的正半轴为极轴建立坐标系，曲线C2的坐标系方程是ρ=2，正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为（2， 
）．
（1）求点A，B，C，D的直角坐标；
（2）设P为C1上任意一点，求t=|PA|2+|PB|2+|PC|2+|PD|2的取值范围．
【答案】
（1）解：点A，B，C，D的极坐标为 
点A，B，C，D的直角坐标为 
（2）设P（x0，y0），则 
为参数）
t=|PA|2+|PB|2+|PC|2+|PD|2=4x2+4y2+16=32+20sin2φ
∵sin2φ∈[0，1]
∴t∈[32，52]
【解析】（1）先根据题意确定点A，B，C，D的极坐标，再转化为对应的直角坐标；（2）先利用参数方程设出点P的坐标，再利用三角函数求得t的取值范围.
【考点精析】利用椭圆的参数方程对题目进行判断即可得到答案，需要熟知椭圆
的参数方程可表示为
．
练习册系列答案
相关题目
