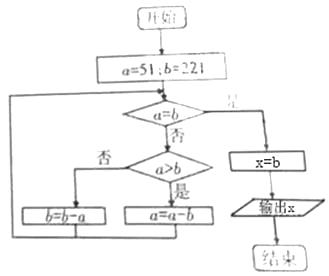
题目内容
【题目】在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分别与
圆O:x2+y2=4交于点A,B,与圆M:(x﹣2)2+(y﹣1)2=1交于点C,D.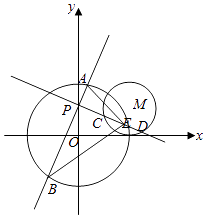
(1)若 ![]() ,求CD的长;
,求CD的长;
(2)若CD中点为E,求△ABE面积的取值范围.
【答案】
(1)解:设直线AB的方程为:y=kx+1(k≠0),
∵ ![]() ,∴
,∴ ![]() +
+ ![]() =22,
=22,
化为:k2=15,
解得k= ![]() .
.
∴直线CD的方程为:y= ![]() x+1.
x+1.
∴|CD|=2  =
= ![]() .
.
(2)①直线AB为y轴时,直线AB的方程为:x=0,直线CD的方程为:y=1.
S△ABE= ![]() =
= ![]() =4.
=4.
②直线AB的斜率存在时,设直线AB的方程为:y=kx+1,
若k=0,则方程为y=1,经过圆心(2,1),此时△ABE不存在,舍去.
k≠0时,可得直线CD的方程为:y=﹣ ![]() x+1.
x+1.
|AB|=2 ![]() =2
=2 ![]() .
.
联立  ,化为:(k2+1)x2﹣4k2x+3k2=0,
,化为:(k2+1)x2﹣4k2x+3k2=0,
△=16k4﹣12(k2+1)k2>0,化为:k2>3.
∴x1+x2= ![]() ,可得E
,可得E ![]() .
.
∴点E到直线AB的距离d=  =
= ![]() .
.
∴S△ABE= ![]() |AB|d=
|AB|d= ![]() ×2
×2 ![]() ×
× ![]() =2
=2 ![]() =2
=2 ![]() ,
,
令k2+1=t>1,可得f(t)= ![]() =
= ![]() ∈(0,2).
∈(0,2).
∴S△ABE∈(0,4).
综上可得:S△ABE∈(0,4].
【解析】(1)本小题主要利用圆中弦长的一半、圆心到弦的距离及圆的半径组成的直角三角形并利用勾股定理来解题;(2)本题的难点在于针对直线AB斜率的进行分类,对于直线的斜率可以分为不存在、存在时为0及存在时不为0.

练习册系列答案
相关题目