题目内容
18.函数y=(sinx-2)(cosx-2)的值域是( )| A. | [$\frac{9}{2}$-2$\sqrt{2}$,$\frac{9}{2}$+2$\sqrt{2}$] | B. | [$\frac{3}{2}$,$\frac{9}{2}$+2$\sqrt{2}$] | C. | [$\frac{3}{2}$,+∞) | D. | [$\frac{9}{2}$-2$\sqrt{2}$,$\sqrt{2}$] |
分析 令t=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)∈[-$\sqrt{2}$,$\sqrt{2}$],可得sinxcosx=$\frac{{t}^{2}-1}{2}$,y=$\frac{1}{2}$(t-2)2+$\frac{3}{2}$,再利用二次函数的性质求得它的值域.
解答 解:函数y=(sinx-2)(cosx-2)=sinx•cosx-2(sinx+cosx)+4,
令t=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)∈[-$\sqrt{2}$,$\sqrt{2}$],可得sinxcosx=$\frac{{t}^{2}-1}{2}$,
y=$\frac{{t}^{2}-1}{2}$-2t+4=$\frac{1}{2}$(t2-4t+4)+$\frac{3}{2}$=$\frac{1}{2}$(t-2)2+$\frac{3}{2}$,
故当t=$\sqrt{2}$时,函数y取得最小值为$\frac{9}{2}$-2$\sqrt{2}$,当t=-$\sqrt{2}$时,函数y取得最大值为$\frac{9}{2}$+2$\sqrt{2}$,
故选:A.
点评 本题主要考查同角三角的基本关系,二次函数的性质,属于中档题.

练习册系列答案
相关题目
8.根据下面程序框图,当n=2时,输出S=( )


| A. | 1000 | B. | 1950 | C. | 2850 | D. | 3800 |
9.设复数z满足z•(2+i)=10-5i(i为虚数单位),则z的共轭复数$\overline{z}$为( )
| A. | -3+4i | B. | -3-4i | C. | 3+4i | D. | 3-4i |
13.若集合A={x|x2-4x<0},B={y|y=2x-5,x∈A},则A∩B等于( )
| A. | ∅ | B. | (0,3) | C. | (-5,4) | D. | (0,4) |
10.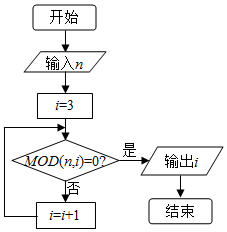 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2,如图所示是一个算法的程序框图,若输出的结果为4,则输入n的值为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2,如图所示是一个算法的程序框图,若输出的结果为4,则输入n的值为( )
 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2,如图所示是一个算法的程序框图,若输出的结果为4,则输入n的值为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2,如图所示是一个算法的程序框图,若输出的结果为4,则输入n的值为( )| A. | 16 | B. | 14 | C. | 12 | D. | 10 |
8.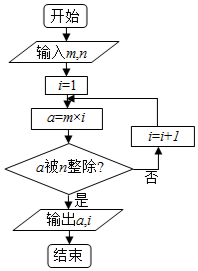 当m=4,n=3时,运行如图所示的程序框图,将输出的a、i代入二项式(x2-$\frac{i}{x}$)a中,则此二项式的展开式中含x3项的系数为( )
当m=4,n=3时,运行如图所示的程序框图,将输出的a、i代入二项式(x2-$\frac{i}{x}$)a中,则此二项式的展开式中含x3项的系数为( )
 当m=4,n=3时,运行如图所示的程序框图,将输出的a、i代入二项式(x2-$\frac{i}{x}$)a中,则此二项式的展开式中含x3项的系数为( )
当m=4,n=3时,运行如图所示的程序框图,将输出的a、i代入二项式(x2-$\frac{i}{x}$)a中,则此二项式的展开式中含x3项的系数为( )| A. | 37${C}_{12}^{7}$ | B. | 38${C}_{12}^{8}$ | C. | -33${C}_{12}^{3}$ | D. | -37${C}_{12}^{5}$ |