题目内容
19．设各项为正数等比数列{an}的前n项和为Sn，已知S1=2，S3=14．（1）求数列{an}的通项公式；
（2）若数列{bn}满足bn=an•log2an，求{bn}的通项公式；
（3）求数列{bn}的前n项和Tn．
分析 （1）设等比数列{an}的公比为q，从而可得S3=a1（1+q+q2）=14，从而解得；
（2）代入an=2n化简即可；
（3）利用错位相减法求和即可．
解答 解：（1）设等比数列{an}的公比为q，
则a1=S1=2，S3=a1（1+q+q2）=14，
解得，q=2或q=-3（舍去）；
故an=2•2n-1=2n；
（2）∵an=2n，
∴bn=an•log2an=n•2n；
（3）Tn=2+2•22+3•23+4•24+5•25+…+n•2n，
2Tn=22+2•23+3•24+4•25+5•26+…+n•2n+1，
两式作差可得，
Tn=-2-22-23-24-25-…-2n+n•2n+1
=-$\frac{2（1-{2}^{n}）}{1-2}$+n•2n+1
=（n-1）2n+1+2．
点评 本题考查了等比数列的性质的应用及错位相减法的应用．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
9．设复数z满足z•（2+i）=10-5i（i为虚数单位），则z的共轭复数$\overline{z}$为（ ）
| A． | -3+4i | B． | -3-4i | C． | 3+4i | D． | 3-4i |
10．
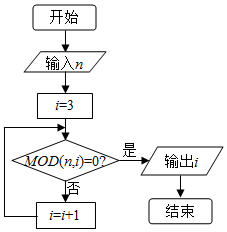已知MOD函数是一个求余函数，其格式为MOD（n，m），其结果为n除以m的余数，例如MOD（8，3）=2，如图所示是一个算法的程序框图，若输出的结果为4，则输入n的值为（ ）
已知MOD函数是一个求余函数，其格式为MOD（n，m），其结果为n除以m的余数，例如MOD（8，3）=2，如图所示是一个算法的程序框图，若输出的结果为4，则输入n的值为（ ）| A． | 16 | B． | 14 | C． | 12 | D． | 10 |
8．
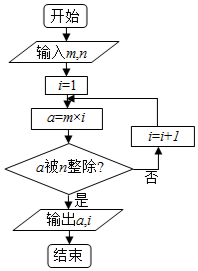当m=4，n=3时，运行如图所示的程序框图，将输出的a、i代入二项式（x2-$\frac{i}{x}$）a中，则此二项式的展开式中含x3项的系数为（ ）
当m=4，n=3时，运行如图所示的程序框图，将输出的a、i代入二项式（x2-$\frac{i}{x}$）a中，则此二项式的展开式中含x3项的系数为（ ）| A． | 37${C}_{12}^{7}$ | B． | 38${C}_{12}^{8}$ | C． | -33${C}_{12}^{3}$ | D． | -37${C}_{12}^{5}$ |