题目内容
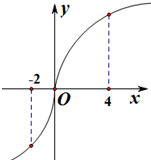已知定义在R上的函数f（x）满足f（4）=f（-2）=1，且y=f′（x）的图象如图所示，则不等式f（x）＜1的解集是（ ）| A、（-2，0） |
| B、（0，4） |
| C、（-2，4） |
| D、（-∞，-2）∪（4，+∞） |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：根据函数的单调性和导数之间的关系，即可得到结论．
解答：
解：由函数的图象可知，当x＞0时，函数f′（x）＞0，函数单调递增，
当x＜0时，函数f′（x）＜0，函数单调递减，且当x=0时，函数取得极小值f（0），
∵f（-2）=f（4）=1，
∴当0≤x＜4时，f（x）＜1，当-2＜x＜0时，f（x）＜1，
综上不等式f（x）＜1的解为当-2＜x＜4时，
即不等式的解集为（-2，4），
故选：C
当x＜0时，函数f′（x）＜0，函数单调递减，且当x=0时，函数取得极小值f（0），
∵f（-2）=f（4）=1，
∴当0≤x＜4时，f（x）＜1，当-2＜x＜0时，f（x）＜1，
综上不等式f（x）＜1的解为当-2＜x＜4时，
即不等式的解集为（-2，4），
故选：C
点评：本题主要考查不等式的解法，利用函数的单调性和导数之间的关系是解决本题的关键．
练习册系列答案
习题精选系列答案
相关题目
已知函数f（x）=ax+x-b的零点x0∈（n，n+1）（n∈Z），其中常数a，b满足0＜b＜1＜a，则n的值为（ ）
| A、2 | B、1 | C、-2 | D、-l |
若定义在R上的函数f（x）=
+x2，则它能取到的最小值为（ ）
| 6 |
| x2+1 |
| A、2 | ||
| B、4 | ||
C、2
| ||
D、2
|
已知正方体ABCD-A1B1C1D1棱长为1，截面AB1D1与平面ABCD相交于直线l，则点B1到直线l的距离为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
cos（-
）=（ ）
| 23π |
| 6 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
设r＞0，那么直线xcosθ+ysinθ=r（θ是常数）与圆
（φ是参数）的位置关系是（ ）
|
| A、相交 | B、相切 |
| C、相离 | D、视r的大小而定 |