题目内容
cos（-
）=（ ）
| 23π |
| 6 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：原式中的角度变形后，利用诱导公式化简，计算即可得到结果．
解答：
解：cos（-
）=cos
=cos（4π-
）=cos（-
）=cos
=
．
故选：A．
| 23π |
| 6 |
| 23π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
故选：A．
点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=sin（4x+φ），x∈[0，2π]的一个零点为
，则f（x）的所有极值点的和为（ ）
| π |
| 8 |
| A、7π | ||
B、
| ||
C、
| ||
| D、9π |
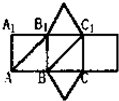如图，正三棱柱的平面展开图，各侧面都是正方形，在这个正三棱柱中：①AB1∥BC1；
②AC1与BC是异面直线；
③AB1与BC所成的角的余弦值为
| ||
| 4 |
④BC1与A1C垂直．
其中正确的是（ ）
| A、①③ | B、②③ | C、②④ | D、②③④ |
函数f（x）=x2-x的零点个数是（ ）
| A、3 | B、2 | C、1 | D、0 |
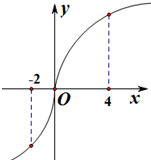已知定义在R上的函数f（x）满足f（4）=f（-2）=1，且y=f′（x）的图象如图所示，则不等式f（x）＜1的解集是（ ）| A、（-2，0） |
| B、（0，4） |
| C、（-2，4） |
| D、（-∞，-2）∪（4，+∞） |
函数f（x）=lg
的图象（ ）
| 1+sinx |
| cosx |
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、关于直线y=x对称 |
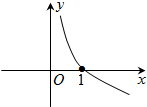已知函数f（x）的导函数图象如图所示，若△ABC是以角C为钝角的钝角三角形，则一定成立的是（ ）| A、f（sinA）＞f（cosB） |
| B、f（sinA）＜f（cosB） |
| C、f（sinA）＞f（sinB） |
| D、f（cosA）＜f（cosB） |