题目内容
13. 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则剩余部分体积与原四棱锥体积的比值为( )
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则剩余部分体积与原四棱锥体积的比值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 根据几何体的三视图可得:该几何体是过BD且平行于PA的平面截四棱锥P-ABCD所得的几何体.设AB=1,则截取的部分为三棱锥E-BCD,V剩余部分=V四棱锥P-ABCD-V三棱锥E-BCD.即可得出.
解答 解:根据几何体的三视图可得;
该几何体是过BD且平行于PA的平面截四棱锥P-ABCD所得的几何体.
设AB=1,则截取的部分为三棱锥E-BCD,
V三棱锥E-BCD=$\frac{1}{3}$×$\frac{1}{2}$×1×1×$\frac{1}{2}$=$\frac{1}{12}$.
V四棱锥P-ABCD=$\frac{1}{3}×{S}_{正方形ABCD}×PA$=$\frac{1}{3}×{1}^{2}×1$=$\frac{1}{3}$.
剩余部分的体积V剩余部分=V四棱锥P-ABCD-V三棱锥E-BCD=$\frac{1}{3}$-$\frac{1}{12}$=$\frac{1}{4}$.
∴剩余部分体积与原四棱锥体积的比值=$\frac{\frac{1}{4}}{\frac{1}{3}}$=$\frac{3}{4}$.
故选:D.
点评 本题考查了四棱锥与四棱锥的三视图及其体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
3.已知偶函数f(x)的定义域为(-1,0)∪(0,1),且$f(\frac{1}{e})=0$.当0<x<1时,(1-x2)ln(1-x2)f'(x)>2xf(x),则满足f(x)<0的x的取值范围是( )
| A. | $(-\frac{1}{e},0)∪(0,\frac{1}{e})$ | B. | $(-\frac{1}{2},0)∪(\frac{1}{2},1)$ | C. | $(-1,-\frac{1}{e})∪(\frac{1}{e},1)$ | D. | $(-1,-\frac{1}{2})∪(0,\frac{1}{2})$ |
1.下列命题中不正确的是( )
| A. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β | |
| D. | 如果平面α⊥平面β,且直线l∥平面α,则直线l⊥平面β |
8.设全集U=R,集合A={x|x2-3x>0},则∁UA=( )
| A. | [0,3] | B. | (0,3) | C. | (-∞,0)∪(3,+∞) | D. | (-∞,0]∪[3,+∞) |
2.函数f(x)=(3-x2)•ln|x|的大致图象为( )
| A. | 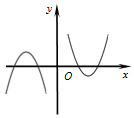 | B. | 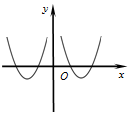 | C. |  | D. | 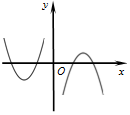 |
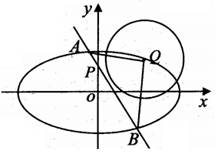 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,圆Q:x2+y2-4x-2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,圆Q:x2+y2-4x-2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.