题目内容
1．下列命题中不正确的是（ ）| A． | 如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么l⊥γ | |
| B． | 如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β | |
| C． | 如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β | |
| D． | 如果平面α⊥平面β，且直线l∥平面α，则直线l⊥平面β |
分析 根据空间中直线与直线，直线与平面位置关系及几何特征，逐一分析给定四个结论的真假，可得答案．
解答 解：如果平面α⊥平面γ，平面β⊥平面γ，α∩β=l，那么l⊥γ，故A正确；
如果平面α⊥平面β，那么平面α内一定存在平行于交线的直线平行于平面β，故B正确；
如果平面α内存在直线垂直于平面β，则平面α⊥平面β，故如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β，故C正确；
如果平面α⊥平面β，且直线l∥平面α，则直线l与平面β的关系不确定，故D错误；
故选：D
点评 本题以命题的真假判断与应用为载体，考查了空间直线与直线，直线与平面位置关系及几何特征，难度中档．
练习册系列答案
相关题目
11．《九章算术•均输》中有如下问题：“今有五人分五钱，令上二人所得与下三人等，问各得几何．”其意思为“已知甲、乙、丙、丁、戊五人分5 钱，甲、乙两人所得与丙、丁、戊三人所得相同，且甲、乙、丙、丁、戊所得依次成等差数列，问五人各得多少钱？”（“钱”是古代的一种重量单位）．这个问题中，乙所得为（ ）
| A． | $\frac{4}{3}$钱 | B． | $\frac{7}{6}$钱 | C． | $\frac{6}{5}$钱 | D． | $\frac{5}{4}$钱 |
12．
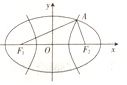如图F1，F2是双曲线${C_1}：{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点，点A是C1，C2在第一象限内的公共点，若|F1F2|=|F1A|，则C2的离心率是（ ）
如图F1，F2是双曲线${C_1}：{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点，点A是C1，C2在第一象限内的公共点，若|F1F2|=|F1A|，则C2的离心率是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{2}{5}$ |
9．已知函数f（x）是定义在R上的奇函数，当x≥0时，$f（x）=\frac{1}{2}（|x-1|+|x-2|-3）$，若?x∈R，f（x-a）≤f（x），则a的取值范围是（ ）
| A． | a≥3 | B． | -3≤a≤3 | C． | a≥6 | D． | -6≤a≤6 |
16．函数f（x）=sin2x+2$\sqrt{3}$cos2x-$\sqrt{3}$，函数g（x）=mcos（2x-$\frac{π}{6}$）-2m+3（m＞0），若存在x1，x2∈[0，$\frac{π}{4}$]，使得f（x1）=g（x2）成立，则实数m的取值范围是（ ）
| A． | （0，1] | B． | [1，2] | C． | [$\frac{2}{3}$，2] | D． | [$\frac{2}{3}$，$\frac{4}{3}$] |
13．
在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为正方形，PA=AB，该四棱锥被一平面截去一部分后，剩余部分的三视图如图，则剩余部分体积与原四棱锥体积的比值为（ ）
在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为正方形，PA=AB，该四棱锥被一平面截去一部分后，剩余部分的三视图如图，则剩余部分体积与原四棱锥体积的比值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
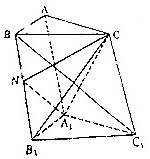如图，在直三棱柱ABC-A1B1 C1中，AC=2$\sqrt{2}$，AB=BC=BB1=2，N是BB1的中点．