题目内容
3.已知偶函数f(x)的定义域为(-1,0)∪(0,1),且$f(\frac{1}{e})=0$.当0<x<1时,(1-x2)ln(1-x2)f'(x)>2xf(x),则满足f(x)<0的x的取值范围是( )| A. | $(-\frac{1}{e},0)∪(0,\frac{1}{e})$ | B. | $(-\frac{1}{2},0)∪(\frac{1}{2},1)$ | C. | $(-1,-\frac{1}{e})∪(\frac{1}{e},1)$ | D. | $(-1,-\frac{1}{2})∪(0,\frac{1}{2})$ |
分析 令g(x)=$\frac{f(x)}{ln(1-{x}^{2})}$,根据已知可判断g(x)=$\frac{f(x)}{ln(1-{x}^{2})}$在(0,1)上为增函数,进而可得f(x)在(0,1)上为减函数,结合函数f(x)为偶函数,且$f(\frac{1}{e})=0$可得答案.
解答 解:令g(x)=$\frac{f(x)}{ln(1-{x}^{2})}$,则g′(x)=$\frac{f′(x)ln(1-{x}^{2})-f(x)•\frac{2x}{1-{x}^{2}}}{l{n}^{2}(1-{x}^{2})}$,
∵当0<x<1时,(1-x2)ln(1-x2)f'(x)>2xf(x),
∴$f′(x)ln(1-{x}^{2})-f(x)•\frac{2x}{1-{x}^{2}}$>0,
即g(x)=$\frac{f(x)}{ln(1-{x}^{2})}$在(0,1)上为增函数,
则f(x)在(0,1)上为减函数,
又由函数f(x)为偶函数,且$f(\frac{1}{e})=0$.
故当x∈$(-1,-\frac{1}{e})∪(\frac{1}{e},1)$时,f(x)<0,
故选:C
点评 本题考查的知识点是函数的奇偶性,函数的单调性,构造法解决函数综合性问题,导数的综合应用,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.《九章算术•均输》中有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5 钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,乙所得为( )
| A. | $\frac{4}{3}$钱 | B. | $\frac{7}{6}$钱 | C. | $\frac{6}{5}$钱 | D. | $\frac{5}{4}$钱 |
12.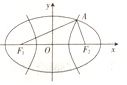 如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
 如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
13. 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则剩余部分体积与原四棱锥体积的比值为( )
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则剩余部分体积与原四棱锥体积的比值为( )
 在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则剩余部分体积与原四棱锥体积的比值为( )
在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB,该四棱锥被一平面截去一部分后,剩余部分的三视图如图,则剩余部分体积与原四棱锥体积的比值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
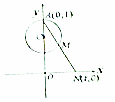 把周长为1的圆的圆心C放在y轴,顶点A(0,1),一动点M从A开始顺时针绕圆运动一周,记走过的弧长$\widehat{AM}$=x,直线AM与x轴交于点N(t,0),则函数t=f(x)的大致图象( )
把周长为1的圆的圆心C放在y轴,顶点A(0,1),一动点M从A开始顺时针绕圆运动一周,记走过的弧长$\widehat{AM}$=x,直线AM与x轴交于点N(t,0),则函数t=f(x)的大致图象( )