题目内容
若直线l不平行于平面α,且l?α,则( )
| A、α内的所有直线与l异面 |
| B、α内不存在与l平行的直线 |
| C、α内存在唯一的直线与l平行 |
| D、α内的直线与l都相交 |
考点:平面的基本性质及推论
专题:计算题,空间位置关系与距离
分析:根据线面关系的定义,我们根据已知中直线l不平行于平面α,且l?α,判断出直线l与α的关系,利用直线与平面相交的定义,我们逐一分析四个答案,即可得到结论.
解答:
解:直线l不平行于平面α,且l?α,则l与α相交
l与α内的直线可能相交,也可能异面,但不可能平行
故A,C,D错误
故选B.
l与α内的直线可能相交,也可能异面,但不可能平行
故A,C,D错误
故选B.
点评:本题考查线线、线面位置关系的判定,考查逻辑推理能力和空间想象能力.其中利用已知判断出直线l与α的关系是解答本题的关键.

练习册系列答案
相关题目
抛物线的顶点为(0,-1),对称轴为y轴,则抛物线的解析式是( )
A、y=-
| ||
B、y=
| ||
| C、y=4x2-16 | ||
| D、y=-4x2+16 |
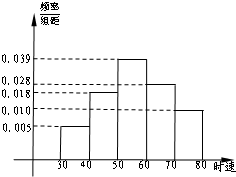 5000辆汽车经过某一雷达测速区,其速度频率分布直方图如图所示,则时速超过70km/h的汽车数量为( )
5000辆汽车经过某一雷达测速区,其速度频率分布直方图如图所示,则时速超过70km/h的汽车数量为( )| A、50 | B、500 |
| C、1000 | D、4500 |
 设函数f(x)=
设函数f(x)=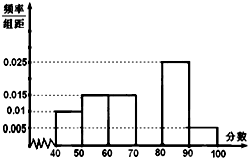 某校从参加高一年级期末考试的学生中抽出20名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100],然后画出如下所示频率分布直方图,但是缺失了第四组[70,80)的信息.观察图形的信息,回答下列问题.
某校从参加高一年级期末考试的学生中抽出20名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100],然后画出如下所示频率分布直方图,但是缺失了第四组[70,80)的信息.观察图形的信息,回答下列问题. 已知某几何体的三视图如图所示,其中正视图是直角三角形,侧视图是正三角形,俯视图是边长为2的正方形,则此几何体的表面积为
已知某几何体的三视图如图所示,其中正视图是直角三角形,侧视图是正三角形,俯视图是边长为2的正方形,则此几何体的表面积为