题目内容
抛物线的顶点为(0,-1),对称轴为y轴,则抛物线的解析式是( )
A、y=-
| ||
B、y=
| ||
| C、y=4x2-16 | ||
| D、y=-4x2+16 |
考点:二次函数的图象
专题:函数的性质及应用
分析:本题主要考查了二次函数的图象的性质,把x=0,分别代入A,B,C,D计算取y的值,即可判断.
解答:
解:∵抛物线的顶点为(0,-1),
∴x=0,y=-1,
而当x=0时,
对于A,y=1,对于B,y=-1,对于C,y=-16,对于D,y=16,
故选:B
∴x=0,y=-1,
而当x=0时,
对于A,y=1,对于B,y=-1,对于C,y=-16,对于D,y=16,
故选:B
点评:本题主要考查了二次函数的图象的性质,属于基础题.

练习册系列答案
相关题目
已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)<
,则f(x)<
+
的解集为( )
| 1 |
| 3 |
| x |
| 3 |
| 2 |
| 3 |
| A、{x|-1<x<1} |
| B、{x|<-1} |
| C、{x|x<-1或x>1} |
| D、{x|x>1} |
若直线l不平行于平面α,且l?α,则( )
| A、α内的所有直线与l异面 |
| B、α内不存在与l平行的直线 |
| C、α内存在唯一的直线与l平行 |
| D、α内的直线与l都相交 |
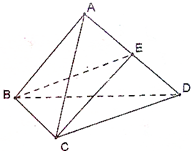 在四面体ABCD中,E为AD中点,△ABC与△BCD都是边长为4的正三角形.
在四面体ABCD中,E为AD中点,△ABC与△BCD都是边长为4的正三角形.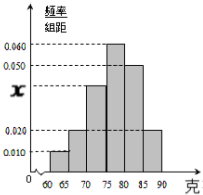 某工厂对一批产品的质量进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图.已知样本中产品净重在[70,75)克的个数是8个.
某工厂对一批产品的质量进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图.已知样本中产品净重在[70,75)克的个数是8个.