Question

10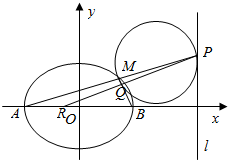．如图，AB是长轴长为6，焦距为2的椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点，直线l的方程为x=9，M是椭圆C上异于A，B的一点，直线AM交l于点P．
（1）求椭圆方程；
（2）以MP为直径的圆与直线MB交于点Q，试证明：直线PQ与x轴的交点R为定点，并求该定点坐标．

Answer 1

分析 （1）由题意可得a=3，c=1，由a，b，c的关系可得b，进而得到椭圆方程；
（2）设M（x₀，y₀），R（t，0），求得直线AM的方程，求得P的坐标，由圆的性质可得MQ⊥PQ，运用直线垂直的条件：斜率之积为-1，求得直线PQ的方程，令y=0，可得交点R的坐标，即可得证．

解答 解：（1）解：由题意可得，a=3，c=1，b=$\sqrt{{a}^{2}-{c}^{2}}$=$2\sqrt{2}$．
∴椭圆C的方程为$\frac{x^2}{9}+\frac{y^2}{8}=1$；     
（2）证明：由（1）知，A（-3，0），B（3，0），
设M（x₀，y₀），R（t，0），
则直线AM的方程为$y=\frac{y_0}{{{x_0}+3}}（x+3）$，
所以点P的坐标为$（9，\frac{{12{y_0}}}{{{x_0}+3}}）$，
由题意，MQ⊥PQ，∴k_MQk_PQ=-1，
∴直线PQ的方程为$y=-\frac{{{x_0}-3}}{y_0}（x-9）+\frac{{12{y_0}}}{{{x_0}+3}}$，
令y=0结合$\frac{x_0^2}{9}+\frac{y_0^2}{8}=1$，得x=$-\frac{5}{3}$，
所以直线PQ与x轴的交点R为定点（-$\frac{5}{3}$，0）．

点评 本题考查椭圆方程的求法，考查直径所对圆的圆周角为直角，以及两直线垂直的条件，以及直线方程的运用，属于中档题．