题目内容
20.已知过点A(1,0)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.(I)求k的取值范围:
(Ⅱ)$\overrightarrow{OM}•\overrightarrow{ON}$=12,其中O为坐标原点,求|MN|.
分析 (Ⅰ)用点斜式求得直线l的方程,根据圆心到直线的距离等于半径求得k的值,可得满足条件的k的范围.
(Ⅱ)由题意可得,经过点M、N、A的直线方程为y=k(x-1),联立直线方程和圆的方程,化为关于x的一元二次方程,利用根与系数的关系求出M,N横纵坐标的积,结合$\overrightarrow{OM}•\overrightarrow{ON}$=12求出直线的斜率,得到直线方程,再由直线过圆心直接得答案.
解答 解:(Ⅰ)设过点A(1,0)的直线方程:y=k(x-1),即:kx-y-k=0.
由已知可得圆C的圆心C的坐标(2,3),半径R=1.
故由$\frac{|2k-3-k|}{\sqrt{{k}^{2}+1}}$=1,解得:k=$\frac{4}{3}$.
故当k>$\frac{4}{3}$时,过点A(1,0)的直线与圆C:(x-2)2+(y-3)2=1相交于M,N两点;
(Ⅱ)设M(x1,y1);N(x2,y2),
由题意可得,经过点M、N、A的直线方程为y=k(x-1),代入圆C的方程(x-2)2+(y-3)2=1,
可得(1+k2)x2-2(k2+3k+2)x+k2+6k+12=0,
∴x1+x2=$\frac{2({k}^{2}+3k+2)}{1+{k}^{2}}$,x1•x2=$\frac{{k}^{2}+6k+12}{1+{k}^{2}}$,
∴y1•y2=k(x1-1)•k(x2-1)=k2[x1x2-(x1+x2)+1]
=${k}^{2}[\frac{{k}^{2}+6k+12}{1+{k}^{2}}-\frac{2{k}^{2}+6k+4}{1+{k}^{2}}+1]$=$\frac{9{k}^{2}}{1+{k}^{2}}$.
由$\overrightarrow{OM}•\overrightarrow{ON}$=12,
得x1•x2+y1•y2=$\frac{10{k}^{2}+6k+12}{1+{k}^{2}}=12$,解得:k=0(舍)或k=3,
故直线l的方程为 y=3x-3.
∵圆心C在直线l上,MN长即为圆的直径,
∴|MN|=2.
点评 本题主要考查直线和圆的位置关系的应用,以及直线和圆相交的弦长公式的计算,考查学生的计算能力,是中档题.

 天天练口算系列答案
天天练口算系列答案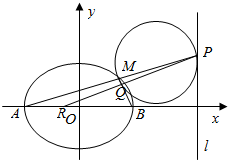 如图,AB是长轴长为6,焦距为2的椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,直线l的方程为x=9,M是椭圆C上异于A,B的一点,直线AM交l于点P.
如图,AB是长轴长为6,焦距为2的椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,直线l的方程为x=9,M是椭圆C上异于A,B的一点,直线AM交l于点P.