题目内容
1.右焦点坐标是(2,0),且经过点(-2,-$\sqrt{2}$)的椭圆的标准方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1.分析 设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得c=2,结合a,b,c的关系和点(-2,-$\sqrt{2}$)代入椭圆方程,解方程可得a,b,进而得到椭圆方程.
解答 解:设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得c=2,即有a2-b2=4,
代入点(-2,-$\sqrt{2}$),可得$\frac{4}{{a}^{2}}$+$\frac{2}{{b}^{2}}$=1,
解得a=2$\sqrt{2}$,b=2.
即有椭圆方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1.
故答案为:$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1.
点评 本题考查椭圆的方程的求法,注意运用待定系数法,考查运算能力,属于基础题.

练习册系列答案
相关题目
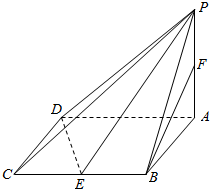 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA⊥面ABCD,PA=$\sqrt{3}$,E,F分别为BC,PA的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA⊥面ABCD,PA=$\sqrt{3}$,E,F分别为BC,PA的中点.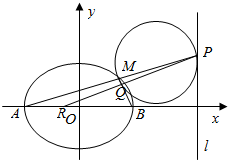 如图,AB是长轴长为6,焦距为2的椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,直线l的方程为x=9,M是椭圆C上异于A,B的一点,直线AM交l于点P.
如图,AB是长轴长为6,焦距为2的椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,直线l的方程为x=9,M是椭圆C上异于A,B的一点,直线AM交l于点P.