题目内容
9．在双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的两条渐近线上各取一点P，Q，若以PQ为直径的圆总过原点，则C的离心率为（ ）| A． | 3 | B． | $\sqrt{5}$ | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
分析 利用已知条件推出渐近线的夹角关系，然后求解双曲线的离心率即可．
解答 解：双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的两条渐近线上各取一点P，Q，
若以PQ为直径的圆总过原点，
可知两条渐近线互相垂直，可得a=b，则c=$\sqrt{2}a$，
所以双曲线的离心率为：$\frac{c}{a}=\sqrt{2}$．
故选：D．
点评 本题考查双曲线的简单性质的应用，考查计算能力．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
如图，已知AB为半圆O的直径，点C为半圆上一点，过点C作半圆的切线CD，过点B作BD⊥CD于点D．求证：BC2=BA•BD．
20．已知平面区域D={（x，y）|$\left\{\begin{array}{l}{x-4y+3≤0}\\{3x+5y-25≤0}\\{x≥1}\end{array}\right.$}，Z=$\frac{y}{x+2}$．若命题“?（x，y）∈D，Z≥m”为真命题，则实数m的最大值为（ ）
| A． | $\frac{22}{15}$ | B． | $\frac{2}{7}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
14．设i为虚数中单位，若复数z=$\frac{a}{1-2i}$+i（a∈R）的实部与虚部互为相反数，则a=（ ）
| A． | -$\frac{5}{3}$ | B． | -$\frac{1}{3}$ | C． | -1 | D． | -5 |
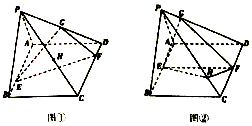
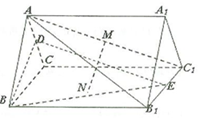如图，正三棱柱ABC-A1B1C1中，侧棱$A{A_1}=\sqrt{3}$，AB=2，D，E分别为棱AC，B1C1的中点，M，N分别为线段AC1和BE的中点．