题目内容
19. 如图,已知AB为半圆O的直径,点C为半圆上一点,过点C作半圆的切线CD,过点B作BD⊥CD于点D.求证:BC2=BA•BD.
如图,已知AB为半圆O的直径,点C为半圆上一点,过点C作半圆的切线CD,过点B作BD⊥CD于点D.求证:BC2=BA•BD.
分析 由弦切角定理可得:∠DCB=∠CAB.进而可得△ACB∽△CDB.即可证明.
解答 证明:CD与半圆相切于点C.
由弦切角定理可得:∠DCB=∠CAB.
∵AB为半圆O的直径,∴∠ACB=90°,
由BD⊥CD,∴∠D=90°,
∴△ACB∽△CDB.
∴$\frac{BC}{BD}$=$\frac{BA}{BC}$,∴BC2=BA•BD.
点评 本题考查了圆的性质、相似三角形的判定与性质定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.已知函数$f(x)=\left\{\begin{array}{l}{2^x}\\ log_2^x\end{array}\right.$$\begin{array}{l}x≤0\\ x>0\end{array}$,若$f(a)=\frac{1}{2}$,则a=( )
| A. | -1 | B. | -1或$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | -1或$-\sqrt{2}$ |
8.已知实数x,y满足的约束条件$\left\{\begin{array}{l}x-2y+2≥0\\ 3x-2y-3≤0\\ x+y-1≥0\end{array}\right.$,表示的平面区域为D,若存在点P(x,y)∈D,使x2+y2≥m成立,则实数m的最大值为( )
| A. | $\frac{181}{16}$ | B. | 1 | C. | $\frac{9}{13}$ | D. | $\frac{1}{2}$ |
9.在双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的两条渐近线上各取一点P,Q,若以PQ为直径的圆总过原点,则C的离心率为( )
| A. | 3 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
 某公路段在某一时刻内监测到的车速频率分布直方图如图所示.
某公路段在某一时刻内监测到的车速频率分布直方图如图所示.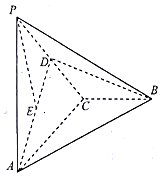 如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为PC的中点,E为AD的中点,PA=AC=2,BC=1.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为PC的中点,E为AD的中点,PA=AC=2,BC=1.