题目内容
6.已知圆C:(x-2)2+y2=9,直线l:x+y=0.(1)求过圆C的圆心且与直线l垂直的直线n的方程;
(2)求与圆C相切,且与直线l平行的直线m的方程.
分析 (1)设直线n的方程为x-y+b=0,利用直线n过圆C的圆心(2,0),求出b,可得直线方程;
(2)由两直线平行时斜率相等,根据直线l方程设所求切线方程为x+y+c=0,由直线与圆相切时,圆心到切线的距离d等于圆的半径r,利用点到直线的距离公式列出关于c的方程,求出方程的解得到c的值,即可确定出直线m的方程.
解答 解:(1)设直线n的方程为x-y+b=0 …(2分)
∵直线n过圆C的圆心(2,0),所以2-0+b=0,∴b=-2
∴直线n的方程为x-y-2=0 …(4分)
(2)∵直线m∥直线x+y=0,
∴设m:x+y+c=0,
∵直线m与圆C相切,
∴3=$\frac{|2+0+c|}{\sqrt{2}}$,
解得:c=-2±3$\sqrt{2}$,
得直线m的方程为:x+y-2+3$\sqrt{2}$=0或x+y-2-3$\sqrt{2}$=0.…(8分)
点评 此题考查了直线与圆的位置关系,以及直线与圆相交的性质,涉及的知识有:点到直线的距离公式,两直线平行、垂直时斜率满足的关系,以及圆的标准方程,属于中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
14.若x∈R,则“x>1”是“$\frac{1}{x}<1$”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
1.下列各式错误的是( )
| A. | 30.8>30.7 | B. | log0.50.4>log0.50.6 | ||
| C. | 0.75-0.1<0.750.1 | D. | log2$\sqrt{3}$>log3$\sqrt{2}$ |
18.设U=R,A={x|2x<1},B={x|log2x<0},则B∩(∁UA)=( )
| A. | {x|x<0} | B. | {x|x>1} | C. | {x|0<x<1} | D. | {x|0<x≤1} |
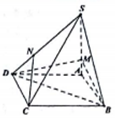 如图,四棱锥S-ABCD中,底面ABCD是边长为4的菱形,∠ABC=60°,SA⊥平面ABCD,且SA=4,M在棱SA上,且AM=1,N在棱SD上且SN=2ND.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的菱形,∠ABC=60°,SA⊥平面ABCD,且SA=4,M在棱SA上,且AM=1,N在棱SD上且SN=2ND. 如图所示,直三棱柱ABC-A1B1C1中,AC=3,AB=BB1=4,BC=5,D为BC的中点.
如图所示,直三棱柱ABC-A1B1C1中,AC=3,AB=BB1=4,BC=5,D为BC的中点.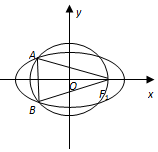 如图,F1是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F1AB是等边三角形,求椭圆的离心率.
如图,F1是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F1AB是等边三角形,求椭圆的离心率.