题目内容
10.已知等比数列{an}中,各项都是正数,且${a_1},\frac{1}{2}{a_3},2{a_2}$成等差数列,则$\frac{{{a_{10}}}}{a_8}$=( )| A. | $\sqrt{2}$ | B. | $3-2\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 设等比数列{an}的公比为q,结合题意可得2×($\frac{1}{2}$a3)=a1+2a2,化简可得q2-2q-1=0,解可得q的值,又由$\frac{{{a_{10}}}}{a_8}$=q2,计算q2的值即可得答案.
解答 解:根据题意,设等比数列{an}的公比为q,
又由${a_1},\frac{1}{2}{a_3},2{a_2}$成等差数列,则有2×($\frac{1}{2}$a3)=a1+2a2;
即2(a1q2)=a1+2a1×q,
变形可得:q2-2q-1=0
解可得q=1+$\sqrt{3}$或q=1-$\sqrt{3}$(舍),
则$\frac{{{a_{10}}}}{a_8}$=q2=(1+$\sqrt{3}$)2=3+2$\sqrt{2}$;
故选:C.
点评 本题考查等比数列的通项公式,关键是求出其公比q的值.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
1.运行如图所示的程序框图,输出的结果S=( )


| A. | 14 | B. | 30 | C. | 62 | D. | 126 |
5.函数f(x)=x4+x2的奇偶性是( )
| A. | 偶函数 | B. | 奇函数 | C. | 非奇非偶 | D. | 无法判断 |
15.一种专门侵占内存的计算机病毒,开机时占据内存2KB,然后每3分钟自身复制一次,复制后所占内存是原来的2倍,若该病毒占据64MB内存(1MB=210KB),则开机后经过( )分钟.
| A. | 45 | B. | 44 | C. | 46 | D. | 47 |
19.如图是用二分法求方程x3-2=0近似解的算法的程序框图,则①②两处应依次填入( )


| A. | a=m,b=m | B. | b=m,a=m | C. | a=f(m),b=f(m) | D. | b=f(m),a=f(m) |
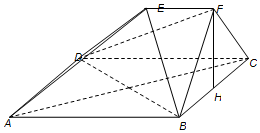 如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点,