题目内容
1．已知θ∈（0，π），且sinθ，cosθ是关于x的方程 5x2-x+m=0的根，求sinθ•cosθ和sin3θ+cos3θ的值．分析 利用根与系数的关系表示出两根之和，两边平方，利用完全平方公式及同角三角函数间的基本关系化简，整理求出sinθ•cosθ的值，利用立方和公式化简sin3θ+cos3θ，整理后将各自的值代入计算即可求出值．
解答 解：由题意得，sinθ+cosθ=$\frac{1}{5}$，即（sinθ+cosθ）2=$\frac{1}{25}$，
整理得：1+2sinθcosθ=$\frac{1}{25}$，
∴sinθ•cosθ=-$\frac{12}{25}$，sin3θ+cos3θ=（sinθ+cosθ）（1-sinθ•cosθ）=$\frac{1}{5}$×（1+$\frac{12}{25}$）=$\frac{37}{125}$．
点评 此题考查了同角三角函数基本关系的运用，熟练掌握同角三角函数间的基本关系是解本题的关键．
练习册系列答案
相关题目
10．为了判断高中生的文理科选修是否与性别有关，随机调查了50名学生，得到如下2×2列联表：
（1）画出列联表的等高条形图，并通过图形判断文理科选修与性别是否有关？
（2）利用列联表的独立性检验，能否在犯错误的概率不超过0.05的前提下认为选修文理科与性别有关？
| 理科 | 文科 | |
| 男 | 14 | 10 |
| 女 | 6 | 20 |
（2）利用列联表的独立性检验，能否在犯错误的概率不超过0.05的前提下认为选修文理科与性别有关？
12．设抛物线y2=2x与过其焦点的直线交于A，B两点，则$\overrightarrow{OA}$•$\overrightarrow{OB}$的值为（ ）
| A． | -$\frac{3}{4}$ | B． | $\frac{3}{4}$ | C． | -3 | D． | 3 |
16．抛物线y=x2上到直线2x-y-4=0距离最近的点的坐标是（ ）
| A． | （1，1） | B． | $（{\frac{1}{2}，\frac{1}{4}}）$ | C． | $（{\frac{1}{3}，\frac{1}{9}}）$ | D． | （2，4） |
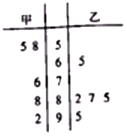某校拟举办“成语大赛”，高一（1）班的甲、乙两名同学在本班参加：“成语大赛”选拔测试，在相同的测试条件下，两人5次测试的成绩（单位：分）的茎叶图如图所示：