题目内容
已知双曲线C:
-
=1(a>0,b>0)离心率为2,它的一个顶点到较近的焦点的距离为1,则该双曲线的渐近线方程为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:双曲线C:
-
=1(a>0,b>0)离心率为2,它的一个顶点到较近的焦点的距离为1,可得
=2,c-a=1,求出a,c,可得b,即可求出双曲线的渐近线方程.
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
解答:
解:∵双曲线C:
-
=1(a>0,b>0)离心率为2,它的一个顶点到较近的焦点的距离为1,
∴
=2,c-a=1,
∴c=2,a=1
∴b=
=
,
∴双曲线的渐近线方程为y=±
x,
故答案为:y=±
x.
| x2 |
| a2 |
| y2 |
| b2 |
∴
| c |
| a |
∴c=2,a=1
∴b=
| c2-a2 |
| 3 |
∴双曲线的渐近线方程为y=±
| 3 |
故答案为:y=±
| 3 |
点评:本题考查双曲线的渐近线方程,考查学生的计算能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
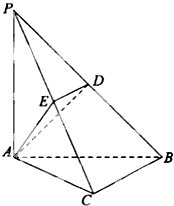 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱PB,PC上,且BC∥平面ADE.
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱PB,PC上,且BC∥平面ADE.