题目内容
19.某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在[50,100]内,发布成绩使用等级制.各等级划分标准见表.规定:A.B.C三级为合格等级,D为不合格等级.| 百分制 | 85以及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
(I)求n和频率分布直方图中的x,y的值;并估计该校高一年级学生成绩是合格等级的概率;
(Ⅱ)在选取的样本中,从A、D两个等级的学生中随机抽取了2名学生进行调研,求至少有一名学生是A等级的概率.
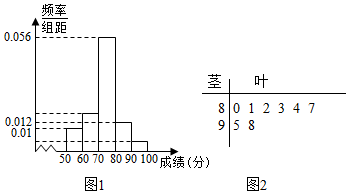
分析 (Ⅰ)由题意知先求出样本容量n,由此能求出频率分布直方图中的x,y的值,估计该校高一年级学生成绩是合格等级的概率.
(Ⅱ)法一:由茎叶图知,A等级学生共有3名,D等级学生共有5名,由此能求出至少有一名学生是A等级的概率.
法二:由茎叶图知,A等级学生共有3名,设为A,B,C,D等级学生共有0.1×50=5名,设为a,b,c,d,e,利用列举法能求出至少有一名学生是A等级的概率.
解答 解:(Ⅰ)由题意知样本容量n=$\frac{6}{0.012×10}$=50,
x=$\frac{2}{50×10}$=0.004,
y=$\frac{1-0.04-0.1-0.12-0.56}{10}$=0.018,
∴成绩是合格等级人数为:(1-0.1)×50=45,
抽取的50人中成绩是合格等级的频率为$\frac{9}{10}$,
依据样本总体的思想,
∴该校高一年级学生成绩是合格等级的概率是$\frac{9}{10}$.
(Ⅱ)(解法一)由茎叶图知,A等级学生共有3名,D等级学生共有0.1×50=5名,
从8名学生中任取2名学生,基本事件总数n=${C}_{8}^{2}$=28,
至少有一名学生是A等级的对立事件是两名学生都是D等级,
∴至少有一名学生是A等级的概率P=1-$\frac{{C}_{5}^{2}}{28}$=$\frac{9}{14}$.
(Ⅱ)(解法二)由茎叶图知,A等级学生共有3名,设为A,B,C,
D等级学生共有0.1×50=5名,设为a,b,c,d,e,
从8名学生中任取2名学生,基本事件有:
AB,AC,Aa,Ab,Ac,Ad,Ae,BC,Ba,Bb,Bc,Bd,Be,Ca,
Cb,Cc,Cd,Ce,ab,ac,ad,ae,bc,bd,be,cd,ce,de,共有28个,
至少有一名学生是A等级的对立事件是两名学生都是D等级,
两名学生都是D等级包含的基本事件有:
ab,ac,ad,ae,bc,bd,be,cd,ce,de,共有10个,
∴至少有一名学生是A等级的概率P=1-$\frac{10}{28}$=$\frac{9}{14}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案| A. | A⊆B | B. | B⊆A | C. | A=B | D. | A∩B=(-∞,2] |
| A. | ($\sqrt{2}$,$\sqrt{6}$) | B. | ($\sqrt{2}$,$\sqrt{7}$) | C. | (2,$\sqrt{6}$) | D. | (2,$\sqrt{7}$) |
| A. | 5 | B. | 6 | C. | 9 | D. | 22 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 的前
的前 项和分别为
项和分别为 ,若
,若 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
