题目内容
已知函数f(x)=x3-3x
(1)求函数在[-1,1]上的最值;
(2)求曲线y=f(x)在点(-1,2)处的切线方程l;
(3)求由切线l,曲线f(x)=x3-3x,x=1围成的面积.
(1)求函数在[-1,1]上的最值;
(2)求曲线y=f(x)在点(-1,2)处的切线方程l;
(3)求由切线l,曲线f(x)=x3-3x,x=1围成的面积.
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由已知得f′(x)=3x2-3,由此利用导数性质能求出函数在[-1,1]上的最大值和最小值.
(2)由k=f′(-1)=3-3=0,利用导数的几何意义能求出曲线y=f(x)在点(-1,2)处的切线方程.(3)由切线l,曲线f(x)=x3-3x,x=1围成的面积S=
(2-x3+3x)dx,由此能求出结果.
(2)由k=f′(-1)=3-3=0,利用导数的几何意义能求出曲线y=f(x)在点(-1,2)处的切线方程.(3)由切线l,曲线f(x)=x3-3x,x=1围成的面积S=
| ∫ | 1 -1 |
解答:
解:(1)∵f(x)=x3-3x,∴f′(x)=3x2-3,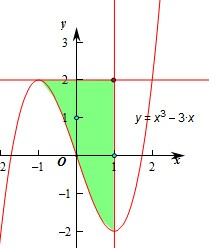 由f′(x)=0,得x1=1,x2=-1,
由f′(x)=0,得x1=1,x2=-1,
∵f(-1)=1-(-3)=4,f(1)=1-3=-2,
∴函数在[-1,1]上的最大值为4,最小值为-2.
(2)∵k=f′(-1)=3-3=0,
∴曲线y=f(x)在点(-1,2)处的切线方程l:
y-2=0.
(3)由切线l:y=2,曲线f(x)=x3-3x,x=1围成的图形如右图:
∴由切线l,曲线f(x)=x3-3x,x=1围成的面积:
S=
(2-x3+3x)dx=(2x-
x4+
x2)
=(2-
+
)-(-2-
+
)
=4.
 由f′(x)=0,得x1=1,x2=-1,
由f′(x)=0,得x1=1,x2=-1,∵f(-1)=1-(-3)=4,f(1)=1-3=-2,
∴函数在[-1,1]上的最大值为4,最小值为-2.
(2)∵k=f′(-1)=3-3=0,
∴曲线y=f(x)在点(-1,2)处的切线方程l:
y-2=0.
(3)由切线l:y=2,曲线f(x)=x3-3x,x=1围成的图形如右图:
∴由切线l,曲线f(x)=x3-3x,x=1围成的面积:
S=
| ∫ | 1 -1 |
| 1 |
| 4 |
| 3 |
| 2 |
| | | 1 -1 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
=4.
点评:本题考查函数最值的求法,考查切线方程的求法,考查曲线围成图形面积的求法,解题时要认真审题,注意定积分的合理运用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
