题目内容
已知函数f（x）=2
sinxcosx+2cos2x-1，（x∈R）．
（1）求函数f（x）的最小正周期．
（2）求函数f（x）在区间[0，
]上的最大值和最小值．
| 3 |
（1）求函数f（x）的最小正周期．
（2）求函数f（x）在区间[0，
| π |
| 2 |
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象
专题：三角函数的图像与性质
分析：（1）利用两角和公式和二倍角公式对函数解析式化简整理，进而根据三角函数的性质求得函数的最小正周期．
（2）根据x的范围，确定2x+
的范围，最后根据三角函数图象和性质求得函数的最大和最小值．
（2）根据x的范围，确定2x+
| π |
| 6 |
解答：
解：（1）f(x)=2
sinxcosx+2cos2x-1=
(2sinxcosx)+2cos2x-1=
sin2x+cos2x=2sin(2x+
)，
∴函数f(x)=2
sinxcosx+2cos2x-1的最小正周期为π．
（2）∵f(x)=2sin(2x+
)在区间[0，
]上为增函数，在[
，
]上为减函数，
又f(0)=1，f(
)=2，f(
)=-1，
∴函数f(x)=2
sinxcosx+2cos2x-1在区间[0，
]上的最大值为2，最
小值为-1．
| 3 |
| 3 |
| 3 |
| π |
| 6 |
∴函数f(x)=2
| 3 |
（2）∵f(x)=2sin(2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
又f(0)=1，f(
| π |
| 6 |
| π |
| 2 |
∴函数f(x)=2
| 3 |
| π |
| 2 |
小值为-1．
点评：本题主要考查了三角函数恒等变换的应用，三角函数图象与性质．考查了学生对三角函数基础知识的灵活运用．
练习册系列答案
阅读快车系列答案
相关题目
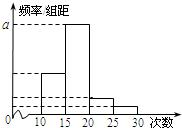对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如图：