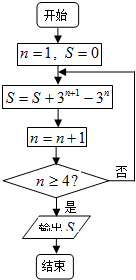
题目内容
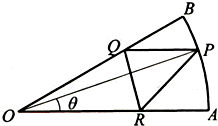 如图,已知扇形AOB是半径为2,圆心角为
如图,已知扇形AOB是半径为2,圆心角为| π |
| 6 |
(Ⅰ)将主题着色板的面积S表示为θ的函数;
(Ⅱ)当角θ取何值时,主题着色板的面积S最大?并求出这个最大值.
考点:三角函数中的恒等变换应用,弧度制的应用
专题:三角函数的图像与性质
分析:(Ⅰ)作PE⊥OA于点E,QF⊥OA于点F,分别表示出PE,OF,进而可表示出EF,进而利用三角形面积公式表示出三角形的面积,并利用二倍角公式和两角和公式化简.
(Ⅱ)根据θ确定2θ+
的范围,进而根据三角函数的性质求得函数的最大值.
(Ⅱ)根据θ确定2θ+
| π |
| 3 |
解答:
解:(Ⅰ)作PE⊥OA于点E,QF⊥OA于点F,
在Rt△OEP中,PE=2sinθ,OE=2cosθ
在Rt△OQF中,OF=
=2
sinθ
∴EF=OE-OF=2cosθ-2
sinθ,
∴S△PQE=
PQ•PE=
EF•PE=
sinθ(2cosθ-2
sinθ)=2sinθcosθ-2
sin2θ=sin2θ-
(1-cos2θ)=sin2θ+
cos2θ-
=2sin(2θ+
)-
,(0<θ<
)
(Ⅱ)∵0<θ<
,所以
<2θ+
<
,
∴当2θ+
=
,即θ=
时,S有最大值且为2-
.
在Rt△OEP中,PE=2sinθ,OE=2cosθ
在Rt△OQF中,OF=
| QF | ||
tan
|
| 3 |
∴EF=OE-OF=2cosθ-2
| 3 |
∴S△PQE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 6 |
(Ⅱ)∵0<θ<
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴当2θ+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 3 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.注重了对学生分析问题和基础知识的掌握.

练习册系列答案
相关题目