题目内容
8.给出下列命题:①若ab>0,a>b,则$\frac{1}{a}$<$\frac{1}{b}$;
②若a>|b|,则a2>b2;
③若a>b,c>d,则a-c>b-d;
④对于正数a,b,m,若a<b,则$\frac{a}{b}<\frac{a+m}{b+m}$
其中真命题的序号是:①②④.
分析 根据不等式的基本性质,判断题目中命题的真假性即可.
解答 解:对于①,若ab>0,则$\frac{1}{ab}$>0
又a>b,
∴$\frac{1}{b}$>$\frac{1}{b}$,∴$\frac{1}{a}$<$\frac{1}{b}$,∴①正确;
对于②,若a>|b|≥0,则a2>b2,∴②正确;
对于③,若a>b,c>d,则-c<-d,
∴-d>-c,∴a-d>b-c,
∴a-c>b-d不成立,③错误;
对于④,对于正数a,b,m,
若a<b,则$\frac{a}{b}<\frac{a+m}{b+m}$成立,
即a(b+m)<b(a+m)
∴am<bm,
∴a<b,④正确;
综上,正确的命题序号是①②④.
故答案为:①②④.
点评 本题考查了不等式的基本性质与应用问题,也考查了命题真假的判断问题,是中档题.

练习册系列答案
相关题目
19.某项体育比赛对前期不同年龄段参赛选手的完成情况进行统计,得到如下2×2的列联表,已知从30~40岁段中随机选出一人,其恰好完成的概率为$\frac{5}{9}$.
(1)完成2×2的列联表;
(2)有多大点把握认为完成比赛与年龄是否有关?
附:下面的临界值表及公式供参考:${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
| 成功(人) | 失败(人) | 合计 | |
| 20~30(岁) | 20 | 40 | 60 |
| 30~40(岁) | 50 | ||
| 合计 | 70 |
(2)有多大点把握认为完成比赛与年龄是否有关?
附:下面的临界值表及公式供参考:${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
3.已知集合A={1,2,3,4},B={x|x=n2,n∈A},则A∩B=( )
| A. | {1} | B. | {1,4} | C. | {1,2} | D. | {0,1,2} |
13.已知n=$\frac{9}{4}$${∫}_{0}^{2}$x2dx,若(1+2x)n=a0+a1x+a2x2+a3x3+a4x4+…+anxn,则a0+a1+a3+a5=( )
| A. | 364 | B. | 365 | C. | 728 | D. | 730 |
20.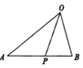 如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )
如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )
 如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )
如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )| A. | $\frac{5}{8}$$\overrightarrow{OB}$+$\frac{3}{8}$$\overrightarrow{OA}$ | B. | $\frac{5}{8}$$\overrightarrow{OA}$+$\frac{3}{8}$$\overrightarrow{OB}$ | C. | $\frac{5}{8}$$\overrightarrow{OB}$-$\frac{3}{8}$$\overrightarrow{OA}$ | D. | $\frac{5}{8}$$\overrightarrow{OA}$-$\frac{3}{8}$$\overrightarrow{OB}$ |